题目内容
8.已知A(-1,1)、B(2,-3),若要在x轴上找一点P,使AP+BP最短,此时点P的坐标为( )| A. | (0,0) | B. | ($\frac{5}{2}$,0) | C. | (-1,0) | D. | (-$\frac{1}{4}$,0) |
分析 求得直线AB的解析式,令y=0可求点P的横坐标.
解答 解:设直线AB的解析式y=kx+b(k≠0),
将点A(-1,1)、B(2,-3)的坐标代入得:$\left\{\begin{array}{l}{-k+b=1}\\{2k+b=-3}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=-\frac{1}{3}}\end{array}\right.$
所以直线AB的解析式为:y=-$\frac{4}{3}$x-$\frac{1}{3}$.
令y=0,解得x=-$\frac{1}{4}$,
所以点P的坐标为(-$\frac{1}{4}$,0),
故选D.
点评 本题综合考查了待定系数法求一次函数解析式,一次函数图象上点的坐标特征,两点之间线段最短等知识点.解题时,注意作图所依据的公理以及相关图形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,直线y=-x+2、y=x-1与两坐标轴围成的四边形是否内接于一个圆?说明理由.
如图,直线y=-x+2、y=x-1与两坐标轴围成的四边形是否内接于一个圆?说明理由. 已知,如图,在△ABC中,CA=CB,AE、BD分别平分∠CAB和∠CBA,交CB、CA于点E、D,EF、DG分别平分∠CED和∠CDE,交CB、CA于点G、F,BD与AE交于点M,EF与DG交于点N,求证:四边形DMEN是菱形.
已知,如图,在△ABC中,CA=CB,AE、BD分别平分∠CAB和∠CBA,交CB、CA于点E、D,EF、DG分别平分∠CED和∠CDE,交CB、CA于点G、F,BD与AE交于点M,EF与DG交于点N,求证:四边形DMEN是菱形.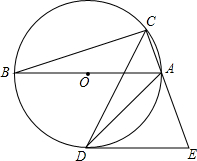 如图,⊙O是△ABC的外接圆,AB为⊙O的直径,∠ACB的平分线交⊙O于点D,点E在CA的延长线上,且DE为⊙O切线.
如图,⊙O是△ABC的外接圆,AB为⊙O的直径,∠ACB的平分线交⊙O于点D,点E在CA的延长线上,且DE为⊙O切线.