题目内容
10.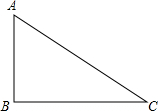 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.(1)尺规作图:作⊙B,使它与AC相切于点D,与BC相交于点E(保留作图痕迹,不写作法,请标明字母.)
(2)在你按(1)中要求所作的图中,若AB=2,∠A=60°,将⊙B与线段CD,CE所围成的部分涂上阴影,并求阴影部分的面积.
分析 (1)过点B作AC的垂线,垂足为点D,然后以B点为圆心,BD为半径作圆即可;
(2)根据已知可求得OC,CD的长,则利用S阴影=S△BCD-S扇形DBE求得阴影部分的面积即可.
解答 解:
(1)如图所示: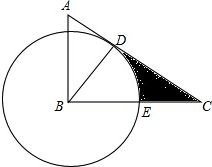
(2)∵AB=2,∠A=60°,
∴∠C=30°,BC=2$\sqrt{3}$,
∴BD=$\sqrt{3}$,AC=4,
∴CD=3,
∵∠C=30°,
∴∠DBC=60°,
∴阴影=S△BCD-S扇形DBE=$\frac{1}{2}$×$\sqrt{3}$×3-$\frac{60π×3}{360}$=$\frac{3\sqrt{3}-π}{2}$.
点评 此题主要考查了对切线的性质及扇形的面积公式,关键是掌握切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线,以及扇形的面积计算公式.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
5.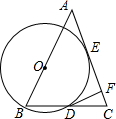 如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.
如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.
(1)求DC的长;(2)求AB的长.
 如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.
如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.(1)求DC的长;(2)求AB的长.
15.下列说法正确的有( )
①将图形A平移后得到图形,则它们是位似图形;
②将图形A绕某点旋转180°后得到图形B,则它们是位似图形;
③两个关于某直线成轴对称的图形一定是位似图形;
④关于某点成中心对称的两个图形一定是位似图形.
①将图形A平移后得到图形,则它们是位似图形;
②将图形A绕某点旋转180°后得到图形B,则它们是位似图形;
③两个关于某直线成轴对称的图形一定是位似图形;
④关于某点成中心对称的两个图形一定是位似图形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.a是$\sqrt{15}$-5的整数部分,则a为( )
| A. | -1 | B. | 1 | C. | 0 | D. | -2 |
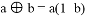 ,若a、b是方程
,若a、b是方程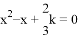 (k<0)的两根,则
(k<0)的两根,则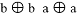 的值为______.
的值为______. 已知实数a,b在数轴上对应点的位置如图所示,化简b-$\sqrt{(a-b)^{2}}$=a.
已知实数a,b在数轴上对应点的位置如图所示,化简b-$\sqrt{(a-b)^{2}}$=a.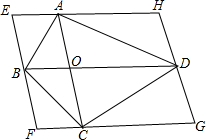 如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.
如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.