题目内容
11. 如图,A,B是⊙O上两点,C为OB延长线上一点,且AB=BC=OB.求证:直线AC与⊙O相切.
如图,A,B是⊙O上两点,C为OB延长线上一点,且AB=BC=OB.求证:直线AC与⊙O相切.
分析 根据已知条件得到△ABO是等边三角形,根据等边三角形的性质得到∠O=∠OAB=∠OBA=60°,由等腰三角形的性质得到∠C=∠BAC,由外角的性质得到∠ABO=∠C+∠BAC=60°,求得∠BAC=30°,得到∠CAO=∠CAB+∠OAB=90°,即可得到结论.
解答 证明:∵AB=OB,
∵OB=AO,
∴AB=OB=AO,
∴△ABO是等边三角形,
∴∠O=∠OAB=∠OBA=60°,
∵AB=BC,
∴∠C=∠BAC,
∵∠ABO=∠C+∠BAC=60°,
∴∠BAC=30°,
∴∠CAO=∠CAB+∠OAB=90°,
∴直线AC与⊙O相切.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.

练习册系列答案
相关题目
2.选用一种多边形形状的瓷砖,用来铺设地面,下列瓷砖形状不可用的是( )
| A. | 正三角形 | B. | 长方形 | C. | 正六边形 | D. | 正八边形 |
20.在-(-8),(-1)2007,-32,0,-|-1|,-$\frac{2}{5}$中,负数的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图所示,已知AB⊥AC,垂足为A,∠1=∠2,∠1与∠B互为余角,证明:AD∥BC∥EF.
如图所示,已知AB⊥AC,垂足为A,∠1=∠2,∠1与∠B互为余角,证明:AD∥BC∥EF. 如图,点A,B在数轴上分别表示有理数a,b,A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离AB=|a-b|
如图,点A,B在数轴上分别表示有理数a,b,A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离AB=|a-b|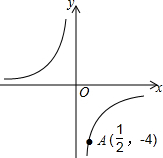 反比例函数y=$\frac{k}{x}$的图象如图所示.
反比例函数y=$\frac{k}{x}$的图象如图所示. 如图,一只小蚂蚁要在正方体的表面从顶点A爬到距A最远的另一个顶点B.哪条路径最短?这样的最短路径有多少条?请说明理由.
如图,一只小蚂蚁要在正方体的表面从顶点A爬到距A最远的另一个顶点B.哪条路径最短?这样的最短路径有多少条?请说明理由. 已知一次函数的图象经过(2,5)和(0,1)两点.
已知一次函数的图象经过(2,5)和(0,1)两点.