题目内容
6. 如图,点A,B在数轴上分别表示有理数a,b,A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离AB=|a-b|
如图,点A,B在数轴上分别表示有理数a,b,A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离AB=|a-b|(1)数轴上表示2和7两点之间的距离是5.
(2)数轴上表示3和-5两点之间的距离是8.
(3)数轴上表示x和-5的两点之间的距离表示为|x+5|,数轴上表示x和3的两点之间的距离表示为
|x-3|.
(4)若|x-3|+|x+5|=8,则x的取值范围是-5≤x≤3.
(5)若x表示-个有理数,则式子8-2|x-3|-2|x-5|有最大值吗?若有,请求出最大值.若没有,说出理由.
分析 (1)根据两点之间的距离公式,即可解答;
(2)根据两点之间的距离公式,即可解答;
(3)根据两点之间的距离公式,即可解答;
(4)根据两点之间的距离公式,即可解答;
(5)把问题转化为:8-2(|x-3|+|x-5|)当|x-3|+|x-5|最小时,代数式有最大值,偶数个点,中间两个点之间的点与线段的端点的距离最小,可得答案.
解答 解:(1)数轴上表示2和7两点之间的距离是:|2-7|=5,故答案为:5;
(2)数轴上表示3和-5两点之间的距离是:|3-(-5)|=8,故答案为:8;
(3)数轴上表示x和-5的两点之间的距离表示为:|x-(-5)|=|x+5|,数轴上表示x和3的两点之间的距离表示为:|x-3|,
故答案为:|x+5|,|x-3|;
(4)若|x-3|+|x+5|=8,则x的取值范围是:-5≤x≤3,故答案为:-5≤x≤3;
(5)根据绝对值的定义有:|x-3|+|x-5|可表示为点x到3与5两点距离之和,
根据几何意义分析可知:当x在3与5之间时,|x-3|+|x-5|有最小值2.
所以8-2|x-3|-2|x-5|=8-2(|x-3|+|x-5|)=8-4=4.
所以代数式式子8-2|x-3|-2|x-5|有最大值4.
点评 本题考查的是绝对值的定义,两点间的距离,理解绝对值的几何意义是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列可以表示y为自变量x的函数的是( )
| A. | f(x)=$\sqrt{x-2}$+$\frac{1}{\sqrt{1-x}}$ | B. | 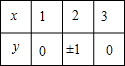 | C. |  | D. | y=1,x∈R |
 如图,CD⊥AB于D,GF⊥AB于F,∠1=50°,求∠2度数.
如图,CD⊥AB于D,GF⊥AB于F,∠1=50°,求∠2度数.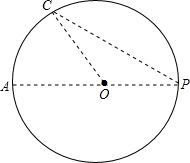 点P到⊙O上的最大距离为10cm.最小距离为5cm.求⊙O的半径.
点P到⊙O上的最大距离为10cm.最小距离为5cm.求⊙O的半径. 如图,A,B是⊙O上两点,C为OB延长线上一点,且AB=BC=OB.求证:直线AC与⊙O相切.
如图,A,B是⊙O上两点,C为OB延长线上一点,且AB=BC=OB.求证:直线AC与⊙O相切.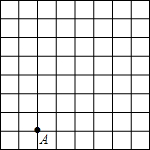 如图,小海龟位于图中点A处,按下述口令移动:前进3格;向右转90°,前进5格;向左转90°,前进3格;向左转90°,前进6格;向右转90°,后退6格;最后向右转90°,前进1格;用粗线将小海龟经过的路线描出来,看一看是什么图形.
如图,小海龟位于图中点A处,按下述口令移动:前进3格;向右转90°,前进5格;向左转90°,前进3格;向左转90°,前进6格;向右转90°,后退6格;最后向右转90°,前进1格;用粗线将小海龟经过的路线描出来,看一看是什么图形.