题目内容
5.已知直线y=kx+b与坐标轴围成的三角形面积是6,且经过(3,0),则这条直线的解析式为y=-$\frac{4}{3}$x+4或y=$\frac{4}{3}$x-4.分析 先根据面积求出三角形在y轴上边的长度,再分正半轴和负半轴两种情况讨论求解.
解答 解:根据题意,设与y轴交点坐标为(0,b)
则$\frac{1}{2}$×3×|b|=6,
解得|b|=4,∴b=±4
①当b=4时,与y轴交点为(0,4)
∴$\left\{\begin{array}{l}{3k+b=0}\\{b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=4}\end{array}\right.$,
∴函数解析式为y=-$\frac{4}{3}$x+4;
②当b=-4时,与y轴的交点为(0,-4)
∴$\left\{\begin{array}{l}{3k+b=0}\\{b=-4}\end{array}\right.$解得$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-4}\end{array}\right.$,
∴函数解析式为y=$\frac{4}{3}$x-4.
∴这个一次函数的解析式是y=-$\frac{4}{3}$x+4或y=$\frac{4}{3}$x-4.
故答案为:y=-$\frac{4}{3}$x+4或y=$\frac{4}{3}$x-4.
点评 本题考查的是待定系数法求一次函数的解析式,先根据三角形面积求出与y轴的交点,再利用待定系数法求函数解析式,本题需要注意有两种情况.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目

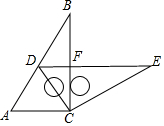 如图,两个含有30°角且大小相同的三角板(Rt△ABC和Rt△DCE)摆放在一起,直角顶点重合,点D刚好落在AB边上.
如图,两个含有30°角且大小相同的三角板(Rt△ABC和Rt△DCE)摆放在一起,直角顶点重合,点D刚好落在AB边上.