题目内容
15.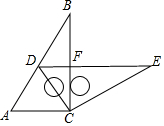 如图,两个含有30°角且大小相同的三角板(Rt△ABC和Rt△DCE)摆放在一起,直角顶点重合,点D刚好落在AB边上.
如图,两个含有30°角且大小相同的三角板(Rt△ABC和Rt△DCE)摆放在一起,直角顶点重合,点D刚好落在AB边上.求证:(1)△ADC为等边三角形;
(2)DE∥AC.
分析 (1)根据题意可得AD=CD,∠A=60°,再根据有一个角等于60°的等腰三角形是等边三角形可得结论;
(2)根据等边三角形的性质可得∠ADC=60°,再证明∠BDE=60°,可得DE∥AC.
解答 证明:(1)∵AD=CD,∠A=60°,
∴△ADC为等边三角形(有一个角等于60°的等腰三角形是等边三角形);
(2)∵△ADC为等边三角形,
∴∠ADC=60°,
∵∠CDE=60°,
∴∠BDE=180°-60°-60°=60°,
∴DE∥AC.
点评 此题主要考查了等边三角形的判定和性质,关键是掌握若从一般三角形出发可以通过三条边相等判定、通过三个角相等判定;若从等腰三角形出发,则想法获取一个60°的角判定.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
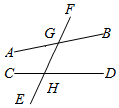 如图,直线EF与AB相交于点G,与CD相交于点H,则∠AGH的对顶角是∠BGF;∠AGF与∠BGH是对顶角;∠AGH与∠AGF和∠BGH是邻补角;∠GHC的邻补角是∠GHD和∠CHE.
如图,直线EF与AB相交于点G,与CD相交于点H,则∠AGH的对顶角是∠BGF;∠AGF与∠BGH是对顶角;∠AGH与∠AGF和∠BGH是邻补角;∠GHC的邻补角是∠GHD和∠CHE.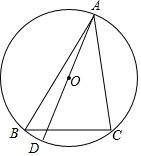 △ABC中,AB=8,BC=5,AC=7.圆O是△ABC的外接圆,AD为直径,连接BD,则AD=$\frac{14\sqrt{3}}{3}$.
△ABC中,AB=8,BC=5,AC=7.圆O是△ABC的外接圆,AD为直径,连接BD,则AD=$\frac{14\sqrt{3}}{3}$.