题目内容
5. 如图,将等腰直角三角形沿虚线裁去顶角后,∠1+∠2=( )
如图,将等腰直角三角形沿虚线裁去顶角后,∠1+∠2=( )| A. | 225° | B. | 235° | C. | 270° | D. | 300° |
分析 先根据等腰直角三角形的性质求出两底角的度数和,再根据四边形内角和定理解答即可.
解答  解:∵△ABC是等腰直角三角形,
解:∵△ABC是等腰直角三角形,
∴∠A+∠B=90°,
∵四边形的内角和是360°,
∴∠1+∠2=360°-(∠A+∠B)=360°-90°=270°.
故选:C.
点评 本题考查的是等腰直角三角形的性质及四边形内角和定理,熟知任意四边形的内角和是360°是解答此题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
16.若x=-3是关于x的方程3x+a=-1的解,则a的值为( )
| A. | 8 | B. | 10 | C. | -8 | D. | -10 |
13.某公司10月份的利润为320万元,要使12月份的利润达到500万元,则平均每月增长的百分率是( )
| A. | 30% | B. | 25% | C. | 20% | D. | 15% |
10. 如图,△ABC内接于⊙O,CD是⊙O的直径,∠A=35°,则∠BCD的度数是( )
如图,△ABC内接于⊙O,CD是⊙O的直径,∠A=35°,则∠BCD的度数是( )
 如图,△ABC内接于⊙O,CD是⊙O的直径,∠A=35°,则∠BCD的度数是( )
如图,△ABC内接于⊙O,CD是⊙O的直径,∠A=35°,则∠BCD的度数是( )| A. | 55° | B. | 65° | C. | 70° | D. | 75° |
17.下列运算中正确的是( )
| A. | (x3)2=x5 | B. | 2a-5•a3=2a8 | C. | 6x3÷(-3x2)=2x | D. | 3-2=$\frac{1}{9}$ |
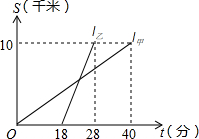 甲、乙两人以相同路线前往距离单位10千米的培训中心参加学习,图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(千米)随时间t(分钟)变化的函数图象.以下说法:①从单位到培训中心,乙比甲少用了30分钟;②甲的平均速度为15千米/小时;③乙走了8千米后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
甲、乙两人以相同路线前往距离单位10千米的培训中心参加学习,图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(千米)随时间t(分钟)变化的函数图象.以下说法:①从单位到培训中心,乙比甲少用了30分钟;②甲的平均速度为15千米/小时;③乙走了8千米后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )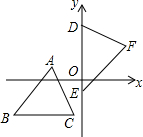 如图,坐标平面上,△ABC≌△FDE,若A点的坐标为(a,1),BC∥x轴,B点的坐标为(b,-3),D、E两点在y轴上,则F点到y轴的距离为4.
如图,坐标平面上,△ABC≌△FDE,若A点的坐标为(a,1),BC∥x轴,B点的坐标为(b,-3),D、E两点在y轴上,则F点到y轴的距离为4.