题目内容
16.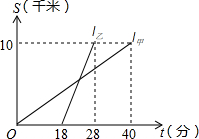 甲、乙两人以相同路线前往距离单位10千米的培训中心参加学习,图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(千米)随时间t(分钟)变化的函数图象.以下说法:①从单位到培训中心,乙比甲少用了30分钟;②甲的平均速度为15千米/小时;③乙走了8千米后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
甲、乙两人以相同路线前往距离单位10千米的培训中心参加学习,图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(千米)随时间t(分钟)变化的函数图象.以下说法:①从单位到培训中心,乙比甲少用了30分钟;②甲的平均速度为15千米/小时;③乙走了8千米后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 ①根据图象即可直接求得两车所用时间,从而判断;
②根据路程是10千米,以及①的结论即可直接求得甲的速度;
③④首先根据待定系数法求得两个函数的解析式,然后求交点即可.
解答 解:①甲所用的时间是40分钟,乙所用的时间是28-18=10分钟,则从单位到培训中心,乙比甲少用了30分钟正确;
②甲的平均速度是$\frac{10}{\frac{40}{60}}$=15km/小时,故命题正确;
③设甲的函数解析式是y=kx,根据题意得:40k=10,
解得:k=$\frac{1}{4}$,则解析式是y=$\frac{1}{4}$x,
设乙的解析式是y=mx+n,
则
$\left\{\begin{array}{l}{28\\;m+\\;n=10}\\{18\\;m+\\;n=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{\\;m=1}\\{\\;n=-18}\end{array}\right.$,
则函数的解析式是y=x-18,
根据题题意得$\left\{\begin{array}{l}{\\;y=\frac{1}{4}\\;x}\\{\\;y=\\;x-18}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{\\;x=24}\\{\\;y=6}\end{array}\right.$,
则24-18=6,
则乙出发24分钟后,路程是6千米处追上甲,则③错误;
乙出发24-18=6分钟后追上甲,④正确.
故选B.
点评 本题主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题,具备在直角坐标系中的读图能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列两个三角形中,一定全等的是( )
| A. | 两个等腰三角形 | B. | 两个等腰直角三角形 | ||
| C. | 两个等边三角形 | D. | 两个周长相等的等边三角形 |
9.估算$\sqrt{6}$的值是在( )
| A. | 1和2之间 | B. | 2和3之间 | C. | 3和4之间 | D. | 4和5之间 |
1.某部队第一天行军5h,第二天行军6h,两天共行军120km,且第二天比第一天多走2km,设第一天和第二天行军的速度分别为xkm/h和ykm/h,则符合题意的二元一次方程是( )
| A. | 5x+6y=118 | B. | 5x=6y+2 | C. | 5x=6y-2 | D. | 5(x+2)=6y |
5. 如图,将等腰直角三角形沿虚线裁去顶角后,∠1+∠2=( )
如图,将等腰直角三角形沿虚线裁去顶角后,∠1+∠2=( )
 如图,将等腰直角三角形沿虚线裁去顶角后,∠1+∠2=( )
如图,将等腰直角三角形沿虚线裁去顶角后,∠1+∠2=( )| A. | 225° | B. | 235° | C. | 270° | D. | 300° |
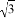 是指坡面的铅直高度BC与水平宽度AC的比,若堤高BC=5m,则坡面AB的长度是( )
是指坡面的铅直高度BC与水平宽度AC的比,若堤高BC=5m,则坡面AB的长度是( )