Question

15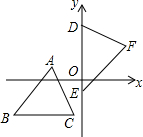．如图，坐标平面上，△ABC≌△FDE，若A点的坐标为（a，1），BC∥x轴，B点的坐标为（b，-3），D、E两点在y轴上，则F点到y轴的距离为4．

Answer 1

分析 如图，作AH⊥BC于H，FP⊥DE于P，根据全等三角形的性质得到AC=DF，∠C=∠FDE，推出△ACH≌△DFP（AAS），根据全等三角形的性质得到AH=FP，根据A点的坐标为（a，1），BC∥x轴，B点的坐标为（b，-3），得到AH=4，即可得到结论．

解答 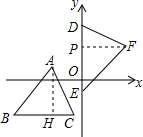解：如图，作AH⊥BC于H，FP⊥DE于P，
∵△ABC≌△FDE，
∴AC=DF，∠C=∠FDE，
在△ACH和△DFP中，
$\left\{\begin{array}{l}{∠C=∠FDP}\\{∠AHC=∠FPD}\\{FD=AC}\end{array}\right.$，
∴△ACH≌△DFP（AAS），
∴AH=FP，
∵A点的坐标为（a，1），BC∥x轴，B点的坐标为（b，-3），
∴AH=4，
∴FP=4，
∴F点到y轴的距离为4，
故答案为：4．

点评 本题考查了坐标与图象的性质的运用，垂直的性质的运用，全等三角形的判定及性质的运用，等腰三角形的性质的运用，解答时证明三角形全等是关键．