题目内容
8.设有n个数x1,x2,x3…xn它们每个数只能取0,1,-2三个数中的一个,且x1+x2+x3+…+xn=-5,x12+x22+x32+…+xn2=19,则x15+x25+x35+…+xn5=-125.分析 根据有n个数x1,x2,x3,…,xn,它们每个数只能取0,1,-2三个数中的一个,且x1+x2+x3+…+xn=-5,可以设其中含有a个-2,则可以得到含有1的个数,然后根据x12+x22+x32+…+xn2=19,可以得到含有的-2的个数与1的个数,从而可以求得x15+x25+x35+…+xn5的值.
解答 解:∵有n个数x1,x2,x3…xn它们每个数只能取0,1,-2三个数中的一个,且x1+x2+x3+…+xn=-5,
∴设在式子x1+x2+x3+…+xn=-5中含有a个-2,则含有2a-5个1,
∵x12+x22+x32+…+xn2=19,
∴(-2)2×a+(2a-5)×12=19,
解得,a=4,
∴2a-5=3,
∴x15+x25+x35+…+xn5=(-2)5×4+15×3=(-32)×4+3=-128+3=-125.
故答案为:-125.
点评 本题考查有理数的混合运算,解题的关键是明确题意,发现其中的规律,找出所求问题需要的条件.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
13.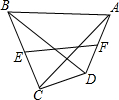 如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
 如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 6 | D. | $\frac{3}{2}\sqrt{3}$ |
18.某地近十天每天平均气温(℃)统计如下:4,3,2,4,4,7,10,11,10,9.关于这10个数据下列说法不正确的是( )
| A. | 众数是4 | B. | 中位数是6 | C. | 平均数是6.4 | D. | 极差是9 |
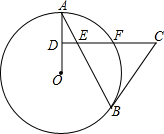 如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB. 已知∠ABC=90°,AB=BC,D为AC上的一点,分别过C点,A点作CE⊥BD于E点,AF⊥BD于F.若EC=5,EF=2,求AF的长.
已知∠ABC=90°,AB=BC,D为AC上的一点,分别过C点,A点作CE⊥BD于E点,AF⊥BD于F.若EC=5,EF=2,求AF的长.