题目内容
20. 如图,已知⊙O是边长为2的等边三角形ABC的外接圆,求⊙O的半径.
如图,已知⊙O是边长为2的等边三角形ABC的外接圆,求⊙O的半径.
分析 连接OB,作OD⊥BC于D,则∠ODB=90°,由等边三角形的性质得出∠OBD=30°,BD=$\frac{1}{2}$BC=1,由三角函数求出OD=$\frac{\sqrt{3}}{3}$BD=$\frac{\sqrt{3}}{3}$,再由含30°角的直角三角形的性质得出OB=2OD,即可得出结果.
解答 解:连接OB,作OD⊥BC于D,如图所示: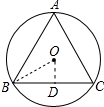
则∠ODB=90°,∠OBD=$\frac{1}{2}$∠ABC=30°,BD=CD=$\frac{1}{2}$BC=1,
∴OD=$\frac{\sqrt{3}}{3}$BD=$\frac{\sqrt{3}}{3}$,
∴OB=2OD=$\frac{2\sqrt{3}}{3}$,
即⊙O的半径为$\frac{2\sqrt{3}}{3}$.
点评 本题考查了等边三角形与圆、等边三角形的性质、三角函数、含30°角的直角三角形的性质;熟练掌握等边三角形的性质,由三角函数求出OD是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若xy=xz成立,则下列式子未必成立的是( )
| A. | y=z | B. | x(y+1)=x(z+1) | C. | xy2=xyz | D. | x(y-1)=x(z-1) |
 已知:如图,AB∥A′B′,BC∥B′C′,B′C′交AB于D,求证:∠B+∠B′=180°.
已知:如图,AB∥A′B′,BC∥B′C′,B′C′交AB于D,求证:∠B+∠B′=180°. 请你表示出阴影部分的面积.并求当a=2,π=3.14时,阴影部分的面积是多少?(精确到0.01)
请你表示出阴影部分的面积.并求当a=2,π=3.14时,阴影部分的面积是多少?(精确到0.01)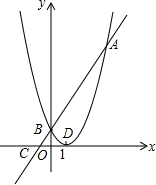 如图,已知抛物线y=(x-1)2与直线y=2x+1相交于A、B两点,与x轴交于点C,顶点为D,
如图,已知抛物线y=(x-1)2与直线y=2x+1相交于A、B两点,与x轴交于点C,顶点为D,