Question

10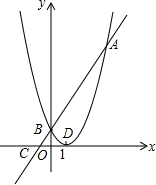．如图，已知抛物线y=（x-1）²与直线y=2x+1相交于A、B两点，与x轴交于点C，顶点为D，
（1）求抛物线与直线交点坐标；
（2）求S_△ABD．

Answer 1

分析 （1）两个函数联立方程组求得交点坐标即可；
（2）利用△ADC的面积减去△BCD的面积得出S_△ABD即可．

解答 解：（1）由题意可知：$\left\{\begin{array}{l}{y=（x-1）^{2}}\\{y=2x+1}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$，$\left\{\begin{array}{l}{x=4}\\{y=9}\end{array}\right.$，
A点坐标为（4，9），B点坐标为（0，1）；
（2）直线y=2x+1与x轴交于点C，坐标为（-$\frac{1}{2}$，0），顶点D为（1，0），
S_△ABD=$\frac{1}{2}$×1×9-$\frac{1}{2}$×$\frac{3}{2}$×1=$\frac{15}{4}$．

点评 此题考查二次函数与一次函数的交点，二次函数的性质，三角形的面积计算方法，两个函数联立方程求得交点坐标是解决问题的关键．