题目内容
已知关于x的一元二次方程x2+(m-2)x+
m-3=0.
(1)求证:无论m取什么实数值,这个方程总有两个不相等的实数根;
(2)若这个方程有一根为x1=1,设这个方程的另一根为x2,求x2与m的值;
(3)设这个方程的两个实数根分别为x1,x2,且满足2x1+x2=m+1,求m的值.
| 1 |
| 2 |
(1)求证:无论m取什么实数值,这个方程总有两个不相等的实数根;
(2)若这个方程有一根为x1=1,设这个方程的另一根为x2,求x2与m的值;
(3)设这个方程的两个实数根分别为x1,x2,且满足2x1+x2=m+1,求m的值.
考点:根的判别式,根与系数的关系
专题:计算题
分析:(1)先计算判别式的值,然后配方得到△=(m-3)2+7,然后根据非负数的性质得到△>0,则可根据判别式的意义判断这个方程总有两个不相等的实数根;
(2)根据根与系数的关系得1+x2=-(m-2),1•x2=
m-3,然后解方程组即可;
(3)根据根与系数的关系得x1+x2=-(m-2),x1•x2=
m-3,而2x1+x2=m+1,先解出x1=2m-1,x2=-3m+3,再得到关于m的方程(2m-1)(-3m+3)=
m-3,然后解方程即可.
(2)根据根与系数的关系得1+x2=-(m-2),1•x2=
| 1 |
| 2 |
(3)根据根与系数的关系得x1+x2=-(m-2),x1•x2=
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)证明:△=(m-2)2-4(
m-3)=m2-6m+16=(m-3)2+7,
∵(m-3)2≥0,
∴△>0,
∴无论m取什么实数值,这个方程总有两个不相等的实数根;
(2)解:根据题意得1+x2=-(m-2),1•x2=
m-3,
∴1+
m-3=-m+2,解得m=
,
∴x2=
•
-3=-
;
(3)解:根据题意得x1+x2=-(m-2),x1•x2=
m-3,
∵2x1+x2=m+1,
∴x1=2m-1,x2=-3m+3,
∴(2m-1)(-3m+3)=
m-3,
整理得6m2-
m=0,
解得m1=0,m2=
.
| 1 |
| 2 |
∵(m-3)2≥0,
∴△>0,
∴无论m取什么实数值,这个方程总有两个不相等的实数根;
(2)解:根据题意得1+x2=-(m-2),1•x2=
| 1 |
| 2 |
∴1+
| 1 |
| 2 |
| 8 |
| 3 |
∴x2=
| 1 |
| 2 |
| 8 |
| 3 |
| 5 |
| 3 |
(3)解:根据题意得x1+x2=-(m-2),x1•x2=
| 1 |
| 2 |
∵2x1+x2=m+1,
∴x1=2m-1,x2=-3m+3,
∴(2m-1)(-3m+3)=
| 1 |
| 2 |
整理得6m2-
| 17 |
| 2 |
解得m1=0,m2=
| 17 |
| 12 |
点评:本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了根与系数的关系.

练习册系列答案
相关题目
若x2+xy=-3,xy+y2=5,则x2+2xy+y2的值为( )
| A、2 | B、-2 | C、8 | D、-8 |
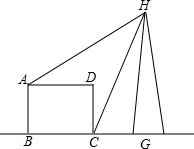 如图所示,形状为长方形的建筑物ABCD的底端BC的长是70cm,高AB=30m,从A,C两点可测得河对面一电视发射塔的顶端H的仰角分别为30°和60°,求塔的高度HG(精确到1m).
如图所示,形状为长方形的建筑物ABCD的底端BC的长是70cm,高AB=30m,从A,C两点可测得河对面一电视发射塔的顶端H的仰角分别为30°和60°,求塔的高度HG(精确到1m). 已知AB是⊙O的一条弦,在圆上作出点C,使得△ABC为等腰三角形(请在图中作出满足条件的所有点C,不写作法,保留作图痕迹).
已知AB是⊙O的一条弦,在圆上作出点C,使得△ABC为等腰三角形(请在图中作出满足条件的所有点C,不写作法,保留作图痕迹).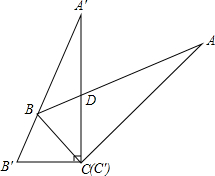 如图,Rt△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C′的位置,使B在斜边A′B′上,A′C与AB相交于D,试确定∠BDC的度数.
如图,Rt△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C′的位置,使B在斜边A′B′上,A′C与AB相交于D,试确定∠BDC的度数.