题目内容
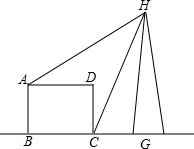 如图所示,形状为长方形的建筑物ABCD的底端BC的长是70cm,高AB=30m,从A,C两点可测得河对面一电视发射塔的顶端H的仰角分别为30°和60°,求塔的高度HG(精确到1m).
如图所示,形状为长方形的建筑物ABCD的底端BC的长是70cm,高AB=30m,从A,C两点可测得河对面一电视发射塔的顶端H的仰角分别为30°和60°,求塔的高度HG(精确到1m).考点:解直角三角形的应用-仰角俯角问题
专题:
分析:首先分析图形,根据题意构造直角三角形;本题涉及到两个直角三角形Rt△AEH、Rt△HCG,应利用其公共边HE,AD=AE-DE构造方程关系式,进而可解即可求出答案.
解答:解:延长AD与HG交于E,设HE=x,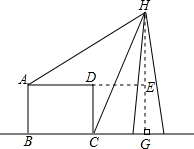
在Rt△ADE中,有HE=AE×tan30°=
AE.
∴AE=
x.
在Rt△HCG中,有CG=HG•cot60°=
HG,
∴HG=
(HE+AB)=
(x+30).
∵CG=DE=AE-AD=
x-70,
∴
×
(x+30)=
x-70,
解得 x=90
+30
∴HG=HE+30=90
+60≈216(m).
答:HG的高约为216m.

在Rt△ADE中,有HE=AE×tan30°=
| ||
| 3 |
∴AE=
| 3 |
在Rt△HCG中,有CG=HG•cot60°=
| ||
| 3 |
∴HG=
| ||
| 3 |
| ||
| 3 |
∵CG=DE=AE-AD=
| 3 |
∴
| ||
| 3 |
| ||
| 3 |
| 3 |
解得 x=90
| 3 |
∴HG=HE+30=90
| 3 |
答:HG的高约为216m.
点评:考查了解直角三角形的应用-仰角俯角问题,本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
下列各式中,去括号正确的是( )
| A、3-(a-b)=3-a+b |
| B、3-2(a-b)=3-2a+b |
| C、3+(a-b)=3+a+b |
| D、3-2(a-b)=3-2a-2b |
若(a-2)2+|b-1|=0,则(b-a)2014的值是( )
| A、2014 | B、-2014 |
| C、1 | D、-1 |
 如图,△ABC中,AB=AC,
如图,△ABC中,AB=AC,
 如图,抛物线y=x2-2x-3与x轴交于A、B两点,直线y=kx-1与抛物线交于P、Q两点,且y轴平分线段PQ,求k的值.
如图,抛物线y=x2-2x-3与x轴交于A、B两点,直线y=kx-1与抛物线交于P、Q两点,且y轴平分线段PQ,求k的值. 如图,MA、MB是⊙O的切线,切点分别为A、B,若∠ACB=65°,则∠AMB=
如图,MA、MB是⊙O的切线,切点分别为A、B,若∠ACB=65°,则∠AMB=