题目内容
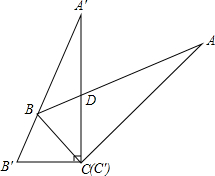 如图,Rt△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C′的位置,使B在斜边A′B′上,A′C与AB相交于D,试确定∠BDC的度数.
如图,Rt△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C′的位置,使B在斜边A′B′上,A′C与AB相交于D,试确定∠BDC的度数.考点:旋转的性质
专题:计算题
分析:先根据旋转的性质得CB=CB′,∠B′=∠ABC=60°,∠A′CB′=∠ACB=90°,则可判断△CBB′为等边三角形,所以∠BCB′=60°,再计算出∠DCB=90°-∠BCB′=30°,然后在△CBD中,利用三角形内角和定理计算∠BDC的度数.
解答:解:∵△ABC以点C为中心旋转到△A′B′C′的位置,使B在斜边A′B′上,
∴CB=CB′,∠B′=∠ABC=60°,∠A′CB′=∠ACB=90°,
∴△CBB′为等边三角形,
∴∠BCB′=60°,
∴∠DCB=90°-∠BCB′=30°,
在△CBD中,∠BDC=180°-∠DBC-∠DCB=90°.
∴CB=CB′,∠B′=∠ABC=60°,∠A′CB′=∠ACB=90°,
∴△CBB′为等边三角形,
∴∠BCB′=60°,
∴∠DCB=90°-∠BCB′=30°,
在△CBD中,∠BDC=180°-∠DBC-∠DCB=90°.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
下列算式中,运算结果为负数的是( )
| A、|-2| |
| B、-(-2) |
| C、(-2)2 |
| D、-22-3 |