题目内容
19. 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=8,AH=6,⊙O的半径OC=5,则AB的值为( )
如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=8,AH=6,⊙O的半径OC=5,则AB的值为( )| A. | 5 | B. | $\frac{13}{2}$ | C. | 7 | D. | $\frac{15}{2}$ |
分析 作直径AE,连接CE,易证得△ABH∽△AEC,然后由相似三角形的对应边成比例计算即可.
解答 解: 作直径AE,连接CE,
作直径AE,连接CE,
∵AE是直径,
∴∠ACE=90°,
∴∠AHB=∠ACE,又∠B=∠E,
∴△ABH∽△AEC,
∴$\frac{AB}{AE}$=$\frac{AH}{AC}$,即$\frac{AB}{10}$=$\frac{6}{8}$,
解得,AB=$\frac{15}{2}$,
故选:D.
点评 此题考查了圆周角定理与相似三角形的判定与性质.掌握圆周角定理、相似三角形的判定定理是解题的关键,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
9. 用一副三角板拼出如图所示的图形,则图中∠α的度数为( )
用一副三角板拼出如图所示的图形,则图中∠α的度数为( )
 用一副三角板拼出如图所示的图形,则图中∠α的度数为( )
用一副三角板拼出如图所示的图形,则图中∠α的度数为( )| A. | 120° | B. | 105° | C. | 100° | D. | 95° |
10. 如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )
如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )
 如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )
如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )| A. | DE是△ABC的中位线 | B. | 点O是△ABC的重心 | ||
| C. | △DEO∽△CBO | D. | $\frac{{S}_{△DOE}}{{S}_{△ADE}}$=$\frac{1}{2}$ |
14.为了了解某班学生每天使用零花钱的情况,随机调查了15名同学,结果如下,下列说法正确的是( )
| 每天零花钱(元) | 0 | 5 | 10 | 15 | 20 |
| 人数 | 2 | 3 | 2 | 6 | 2 |
| A. | 众数是20元 | B. | 平均数是11元 | C. | 极差是15元 | D. | 中位数是10元 |
4.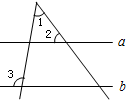 如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )
如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )
 如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )
如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )| A. | 35° | B. | 40° | C. | 45° | D. | 55° |
11. 六个大小相同的正方体搭成的几何体如图所示,其左视图是( )
六个大小相同的正方体搭成的几何体如图所示,其左视图是( )
 六个大小相同的正方体搭成的几何体如图所示,其左视图是( )
六个大小相同的正方体搭成的几何体如图所示,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
8.在我县中学生春季田径运动会上,参加男子跳高的16名运动员的成绩如下表所示:
这些运动员跳高成绩的中位数和众数分别是( )
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 3 | 3 | 4 | 3 | 2 |
| A. | 1.70,1.65 | B. | 1.70,1.70 | C. | 1.65,1.70 | D. | 3,3 |