题目内容

4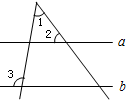．如图，直线a∥b，若∠1=50°，∠3=95°，则∠2的度数为（　　）
A．35°B．40°C．45°D．55°

分析 根据三角形的一个外角等于与它不相邻的两个内角的和，得到∠4的度数，再根据平行线的性质，即可得出∠2的度数．

解答 解：根据三角形外角性质，可得∠3=∠1+∠4，
∴∠4=∠3-∠1=95°-50°=45°，
∵a∥b，
∴∠2=∠4=45°．
故选：C．

点评 本题考查了平行线的性质，以及三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质并准确识图是解题的关键．

练习册系列答案
相关题目
14．半径为6的圆中，120°的圆心角所对的弧长是（　　）
A．4πB．5πC．6πD．8π
15．如图1，在平面直角坐标系中，抛物线y=-$\frac{1}{4}$x2+bx+c经过点S（0，6）和点T（8，6），ST的垂直平分线交抛物线于点B．交x轴交于点C，以BC为直径作⊙P，交y轴于点A，M（点A在点M的下方）．
（1）求该抛物线的解析式；
（2）求出点A的坐标；
（3）如图2，在射线AB上有一动点D，在直线BC上有一动点E，若△ACD的重心为F，且以点A，F，D，E为顶点的四边形是平行四边形，求AF的长．
12．2017-1的计算结果是（　　）
A．-2017B．2016C．$-\frac{1}{2017}$D．$\frac{1}{2017}$
19．如图，△ABC内接于⊙O，AH⊥BC于点H，若AC=8，AH=6，⊙O的半径OC=5，则AB的值为（　　）
A．5B．$\frac{13}{2}$C．7D．$\frac{15}{2}$
9．下列运算正确的是（　　）
A．a2•a3=a6B．a6-a2=a4C．（a2）3=a6D．（a+1）2=a2+1
16．已知关于x的分式方程$\frac{m}{x-2}$-$\frac{x+m}{x+2}$=1的解为正数，则m的取值范围是-$\frac{9}{8}$≤m＜-1．
13．某纸扇的半径为25cm，圆心角为120°，则其面积为$\frac{625}{3}π$cm2．
14．下列图案中，可以看做是中心对称图形的有（　　）
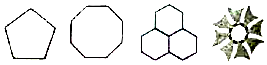
A．1个B．2个C．3个D．4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网