题目内容
7.解方程组:$\left\{\begin{array}{l}{x=\frac{y}{2}=\frac{z}{3}}\\{x+y+z=24}\end{array}\right.$.分析 方程组整理后,利用代入消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{x=\frac{y}{2}=\frac{z}{3}①}\\{x+y+z=24②}\end{array}\right.$,
由①得:y=2x,z=3x,
代入②得:x+2x+3x=24,
解得:x=4,
把x=4代入得:y=8,z=12,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=8}\\{z=12}\end{array}\right.$.
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | (a+b)(b-a)=a2-b2 | B. | (a-b)2=a2-b2 | ||
| C. | (2x-y)2=4x2-2xy+y2 | D. | (x-2y)(-2y-x)=4y2-x2 |
2.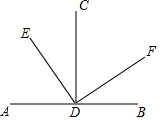 如图AB⊥CD.垂足为D,ED⊥DF,下列结论正确的有( )
如图AB⊥CD.垂足为D,ED⊥DF,下列结论正确的有( )
(1)∠ADE=∠CDF(2)∠EDC=∠FDB(3)∠ADE与∠BDF互余(4)∠CDF与∠ADE互补.
 如图AB⊥CD.垂足为D,ED⊥DF,下列结论正确的有( )
如图AB⊥CD.垂足为D,ED⊥DF,下列结论正确的有( )(1)∠ADE=∠CDF(2)∠EDC=∠FDB(3)∠ADE与∠BDF互余(4)∠CDF与∠ADE互补.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.2017-1的计算结果是( )
| A. | -2017 | B. | 2016 | C. | $-\frac{1}{2017}$ | D. | $\frac{1}{2017}$ |
19. 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=8,AH=6,⊙O的半径OC=5,则AB的值为( )
如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=8,AH=6,⊙O的半径OC=5,则AB的值为( )
 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=8,AH=6,⊙O的半径OC=5,则AB的值为( )
如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=8,AH=6,⊙O的半径OC=5,则AB的值为( )| A. | 5 | B. | $\frac{13}{2}$ | C. | 7 | D. | $\frac{15}{2}$ |
17.已知a,b为两个连续整数,且a<$\sqrt{19}$-1<b,则这两个整数是( )
| A. | 1和2 | B. | 2和3 | C. | 3和4 | D. | 4和5 |
 如图,AD是Rt△ABC斜边上的高,求证:AB2=BD•BC.
如图,AD是Rt△ABC斜边上的高,求证:AB2=BD•BC.