题目内容
9.一个菱形,相邻的两个内角的度数比是1:2,较长的对角线长是6,取两条对角线所在的直线为坐标轴,求四个顶点坐标.分析 本题应分两种情况讨论,当AC=6,或BD=6两种情况讨论.
解答  解:相邻的两个内角的度数比是1:2,则较小角的度数60°.
解:相邻的两个内角的度数比是1:2,则较小角的度数60°.
当较长对角线长是6时,较短的对角线长是:2$\sqrt{3}$.
当AC=6时,A(-3,0),C(3,0),又内角比为1:2,
∴B(0,-$\sqrt{3}$),D(0,$\sqrt{3}$)
或当BD=6时,B(0,-3),D(0,3),又内角比为1:2,
∴C($\sqrt{3}$,0),A(-$\sqrt{3}$,0).
故答案为A(-3,0),B(0,-$\sqrt{3}$),C(3,0),D(0,$\sqrt{3}$)或A(-$\sqrt{3}$,0),B(0,-3),C($\sqrt{3}$,0),D(0,3).
点评 本题考查了菱形的计算以及坐标与图形性质:利用点的坐标求线段的长和判断线段与坐标轴的位置关系.

练习册系列答案
相关题目
19. 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=8,AH=6,⊙O的半径OC=5,则AB的值为( )
如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=8,AH=6,⊙O的半径OC=5,则AB的值为( )
 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=8,AH=6,⊙O的半径OC=5,则AB的值为( )
如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=8,AH=6,⊙O的半径OC=5,则AB的值为( )| A. | 5 | B. | $\frac{13}{2}$ | C. | 7 | D. | $\frac{15}{2}$ |
17.已知a,b为两个连续整数,且a<$\sqrt{19}$-1<b,则这两个整数是( )
| A. | 1和2 | B. | 2和3 | C. | 3和4 | D. | 4和5 |
4.已知圆锥的底面半径为4,母线长为12,则圆锥的侧面展开图的圆心角为( )
| A. | 60° | B. | 90° | C. | 120° | D. | 216° |
14.下列图案中,可以看做是中心对称图形的有( )
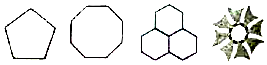

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.若分式$\frac{x+2}{x-1}$有意义,则x的取值范围是( )
| A. | x≥1 | B. | x≠1 | C. | x≥-2 | D. | x≠-2 |
18.下列根式中不是最简二次根式的是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{12}$ | C. | $\sqrt{14}$ | D. | $\frac{\sqrt{17}}{2}$ |
20.下列说法正确的是( )
| A. | 一个数的相反数一定是负数 | B. | 若|a|=|b|,则a=b | ||
| C. | 若|m|=2,则m=±2 | D. | -a一定是负数 |
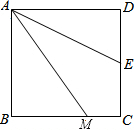 如图,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
如图,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.