题目内容
9．
用一副三角板拼出如图所示的图形，则图中∠α的度数为（ ）| A． | 120° | B． | 105° | C． | 100° | D． | 95° |
分析 先根据直角三角形的性质得出∠BAE及∠E的度数，再由三角形内角和定理及对顶角的性质即可得出结论．
解答 
解：∵图中是一副直角三角板，
∴∠BAE=45°，∠E=30°，
∴∠AFE=180°-∠BAE-∠E=105°，
∴∠α=105°．
故选B．
点评 本题考查的是三角形外角的性质，三角形内角和定理，即三角形内角和是180°．
练习册系列答案
相关题目
20．
如图，OA⊥OC，OB⊥OD，四位同学分别说了自己的观点．甲：∠AOB=∠COD，乙：∠BOC+∠AOD=180°，丙：∠AOB与∠COD都是∠BOC的余角，丁：图中小于平角的角有4个，其中正确的结论有（ ）
如图，OA⊥OC，OB⊥OD，四位同学分别说了自己的观点．甲：∠AOB=∠COD，乙：∠BOC+∠AOD=180°，丙：∠AOB与∠COD都是∠BOC的余角，丁：图中小于平角的角有4个，其中正确的结论有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
17．下列计算正确的是（ ）
| A． | （a+b）（b-a）=a2-b2 | B． | （a-b）2=a2-b2 | ||
| C． | （2x-y）2=4x2-2xy+y2 | D． | （x-2y）（-2y-x）=4y2-x2 |
4．若a+b+c=0，且abc≠0，则a（$\frac{1}{b}$+$\frac{1}{c}$）+b（$\frac{1}{a}$+$\frac{1}{c}$）+c（$\frac{1}{a}$+$\frac{1}{b}$）的值为（ ）
| A． | 1 | B． | 0 | C． | -1 | D． | -3 |
14．半径为6的圆中，120°的圆心角所对的弧长是（ ）
| A． | 4π | B． | 5π | C． | 6π | D． | 8π |
1．
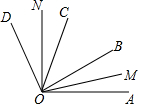如图，已知射线OM，ON分别平分∠AOB，∠COD，若∠MON=α，∠BOC=β，则∠AOD=（ ）
如图，已知射线OM，ON分别平分∠AOB，∠COD，若∠MON=α，∠BOC=β，则∠AOD=（ ）| A． | 2α | B． | 2α-β | C． | α+β | D． | α-β |
如图，AD是Rt△ABC斜边上的高，求证：AB2=BD•BC．
19．
如图，△ABC内接于⊙O，AH⊥BC于点H，若AC=8，AH=6，⊙O的半径OC=5，则AB的值为（ ）
如图，△ABC内接于⊙O，AH⊥BC于点H，若AC=8，AH=6，⊙O的半径OC=5，则AB的值为（ ）| A． | 5 | B． | $\frac{13}{2}$ | C． | 7 | D． | $\frac{15}{2}$ |