题目内容
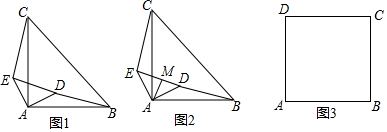
12.若两个相似三角形的相似比是2:3,则它们的对应高线的比是2:3.分析 根据似三角形对应高的比等于相似比解答.
解答 解:两个相似三角形的相似比是2:3,
∴它们的对应高线的比是2:3,
故答案为:2:3.
点评 本题考查的是相似三角形的性质,掌握似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
20.将二次函数y=2x2-4x-1的图象向右平移3个单位,则平移后的二次函数的顶点是( )
| A. | (-2,-3) | B. | (4,3) | C. | (4,-3) | D. | (1,0) |
4.整数m满足$\left\{\begin{array}{l}{2m-1>0}\\{4-2m>-1}\end{array}\right.$,则关于x的方程m2x2-4x-2=(m+2)x2+3x+4的解为( )
| A. | x1=-2,x2=-$\frac{3}{2}$ | B. | x1=2,x2=$\frac{3}{2}$ | ||
| C. | x1=-$\frac{6}{7}$ | D. | x1=-2,x2=-$\frac{3}{2}$,x3=-$\frac{6}{7}$ |
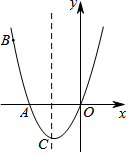 如图,已知抛物线C1经过A(-2,0),B(-3,3)及原点O,顶点为C.
如图,已知抛物线C1经过A(-2,0),B(-3,3)及原点O,顶点为C.