题目内容
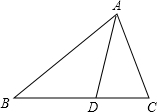 △ABC中,D是BC上一点,若
△ABC中,D是BC上一点,若| S△ABD |
| S△ABC |
| S△ACD |
| S△ABD |
(1)求证:若AD为△ABC的黄金分割线,则D是BC的黄金分割点;
(2)若S△ABC=20,求△ACD的面积.(结果保留根号)
考点:黄金分割
专题:新定义
分析:(1)先由等高的两个三角形面积之比等于底之比,可得
=
,
=
,又因为
=
,等量代换得出
=
,根据黄金分割点的定义即可证明D是BC的黄金分割点;
(2)由(1)知
=
,那么BD=
BC,DC=BC-BD=BC-
BC=
BC,又等高的两个三角形面积之比等于底之比
=
=
,将S△ABC=20代入,即可求出△ACD的面积.
| S△ABD |
| S△ABC |
| BD |
| BC |
| S△ACD |
| S△ABD |
| CD |
| BD |
| S△ABD |
| S△ABC |
| S△ACD |
| S△ABD |
| BD |
| BC |
| CD |
| BD |
(2)由(1)知
| BD |
| BC |
| CD |
| BD |
| ||
| 2 |
| ||
| 2 |
3-
| ||
| 2 |
| S△ACD |
| S△ABC |
| DC |
| BC |
3-
| ||
| 2 |
解答:(1)证明:∵
=
,
=
,
又∵
=
,
∴
=
,
∴D是BC的黄金分割点;
(2)解:由(1)知
=
,
∴BD=
BC,
∴DC=BC-BD=BC-
BC=
BC,
∵
=
=
,
∴S△ACD=
S△ABC=
×20=30-10
.
| S△ABD |
| S△ABC |
| BD |
| BC |
| S△ACD |
| S△ABD |
| CD |
| BD |
又∵
| S△ABD |
| S△ABC |
| S△ACD |
| S△ABD |
∴
| BD |
| BC |
| CD |
| BD |
∴D是BC的黄金分割点;
(2)解:由(1)知
| BD |
| BC |
| CD |
| BD |
∴BD=
| ||
| 2 |
∴DC=BC-BD=BC-
| ||
| 2 |
3-
| ||
| 2 |
∵
| S△ACD |
| S△ABC |
| DC |
| BC |
3-
| ||
| 2 |
∴S△ACD=
3-
| ||
| 2 |
3-
| ||
| 2 |
| 5 |
点评:本题考查了黄金分割的概念:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值(
)叫做黄金比.也考查了三角形的面积.
| ||
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知2a=3b,则
的值为( )
| b |
| a |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
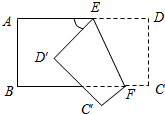 如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠AED′=50°,则∠EFB等于( )
如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠AED′=50°,则∠EFB等于( )| A、50° | B、55° |
| C、60° | D、65° |
 如图,点P是△ABC中,∠B、∠C对角线的交点,∠A=102°,则∠BPC的度数为( )
如图,点P是△ABC中,∠B、∠C对角线的交点,∠A=102°,则∠BPC的度数为( )| A、39° | B、78° |
| C、102° | D、141° |
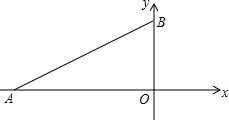 如图,在平面直角坐标系中,点A(-6,0),点B(0,2
如图,在平面直角坐标系中,点A(-6,0),点B(0,2



