Question

4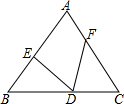．已知，如图，等腰△ABC中，AB=AC，BE=CD，BD=CF．
（1）求证：∠A+2∠EDF=180°；
（2）作∠C的平分线交DF于点G，∠BED=2∠DFC，DG=3，BC=16，求BE长．

Answer 1

分析 （1）首先证明△BED≌△CDF，然后根据全等三角形的对应角相等以及三角形内角和定理证明∠C=∠EDF，据此即可证得；
（2）在FC上截取CM=CD，CG是∠C的平分线，即可证明△DCG≌△MCG，证明GM=FM，然后根据BC=BD+CD列方程求解．

解答 （1）证明：∵AB=AC，
∴∠B=∠C=$\frac{180°-∠A}{2}$，
在△BED和△CDF中，
$\left\{\begin{array}{l}{BE=CD}\\{∠B=∠C}\\{BD=CF}\end{array}\right.$，
∴△BED≌△CDF，
∴∠DFC=∠BDE，
∴∠EDF=180°-（∠BDE+∠FDC）=180°-（∠DFC+∠FDC），
又∵△CDF中，∠DFC+∠FDC=180°-∠C，
∴∠EDF=180°-（180°-∠C）=∠C．
∵∠C=$\frac{180°-∠A}{2}$，
∴∠EDF=$\frac{180°-∠A}{2}$，
∴∠A+2∠EDF=180°；
（2）解：∵△BED≌△CDF，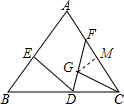
∴∠BDE=∠DFC，∠BED=∠FDC，
∵∠BED=2∠DFC，
设∠BED=∠DFC=x°，
∴∠BED=2x°=∠FDC，
在FC上截取CM=CD，CG是∠C的平分线，
∴∠DCG=∠GCM，
在△DCG和△MCG中，
$\left\{\begin{array}{l}{CM=CD}\\{∠DCG=∠MCG}\\{CG=CG}\end{array}\right.$，
∴△DCG≌△MCG，
∴DG=DM=3，DC=CM，∠DGC=∠GMC=2x，
∴∠FGM=∠GMC-∠GFM=2x-x=x，
∴∠FGM=∠FGM，
∴GM=FM=3，
设CD=EB=y，则FC=3+y=BD，BC=BD+CD=3+y+y，
∴16=3+2y，
则y=$\frac{13}{2}$，即BE=$\frac{13}{2}$．

点评 本题考查了全等三角形的判定与性质，以及等腰三角形的判定与性质，正确作出辅助线是本题的关键．