题目内容
16.用换元法解方程2x2+$\sqrt{{x}^{2}-5x}$=5(2x+3).若设$\sqrt{{x}^{2}-5x}$=y.则原方程可化为关于y的整式方程为2y2+y-15=0.分析 先把原方程转化为2(x2-5x)+$\sqrt{{x}^{2}-5x}$-15=0的形式,然后设$\sqrt{{x}^{2}-5x}$=y,则x2-5x=y2,由此将原方程转化为关于y的方程即可.
解答 解:由2x2+$\sqrt{{x}^{2}-5x}$=5(2x+3),得
2(x2-5x)+$\sqrt{{x}^{2}-5x}$-15=0,
设$\sqrt{{x}^{2}-5x}$=y,则原方程转化为:2y2+y-15=0.
故答案是:$\sqrt{{x}^{2}-5x}$;2y2+y-15=0.
点评 本题主要考查了换元法,即把某个式子看作一个整体,用一个字母去代替它,实行等量替换.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
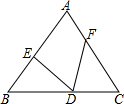 已知,如图,等腰△ABC中,AB=AC,BE=CD,BD=CF.
已知,如图,等腰△ABC中,AB=AC,BE=CD,BD=CF.
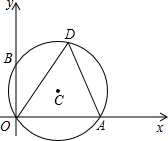 如图,⊙C经过坐标原点O,点B的坐标是(0,2),∠ODA=60°.
如图,⊙C经过坐标原点O,点B的坐标是(0,2),∠ODA=60°.