题目内容
9.已知直线m和位于直线两侧的点A和点B,在直线m上找一点C,使得CA和CB之差最大.画出图形,说明理由.分析 作点A关于直线m的对称点A′,连接A′B并延长交直线m于P,点P即为所求.在m上任意取点P′,再根据三角形的三边关系即可得出结论.
解答 解:作法:作点A关于直线m的对称点A′,连接A′B并延长交直线m于P,点P即为所求.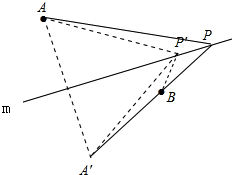
理由:连接PA.
∵PA=PA′,
∴PA-PB=PA′-PB=A′B.
在直线m上另取一点Pˊ,连接P′A、P′A′、P′B,得P′A=P′A′.
在△A′B P′中,P′A′-P′B<A′B,即P′A-P′B<A′B
∴P′A-P′B<PA′-PB,即P′A-P′B<PA-PB,
∴当点A′、B、P在同一条直线上时PA-PB的值最大.
点评 本题考查的是轴对称图形的性质,解答此类题目的关键是根据轴对称的性质画出图形,再由三角形两边之差小于第三条边进行证明即可.

练习册系列答案
相关题目
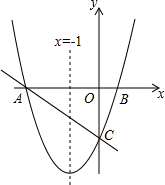 如图,对称轴为直线x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中A点的坐标为(-3,0),C为抛物线与y轴的交点且S△ABC=6
如图,对称轴为直线x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中A点的坐标为(-3,0),C为抛物线与y轴的交点且S△ABC=6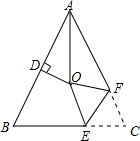 如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为108度.
如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为108度.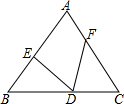 已知,如图,等腰△ABC中,AB=AC,BE=CD,BD=CF.
已知,如图,等腰△ABC中,AB=AC,BE=CD,BD=CF. 如图,D是△ABC中BC边上任意一点,求证:2AD<AB+BC+AC.
如图,D是△ABC中BC边上任意一点,求证:2AD<AB+BC+AC.