题目内容
102×98等于_______；
9996
【解析】102×98=（100+2）×（100-2）=10000-4=9996.
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
如图，在等腰△ABC中，AB=AC，BD⊥AC，∠ABC=72°，则∠ABD=（ ）
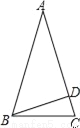
A. 36° B. 54° C. 18° D. 64°
B
【解析】试题分析：根据等腰三角形的性质由已知可求得∠A=36°，再根据垂直的定义和三角形内角和定理不难求得∠ABD=90°﹣36°=54°．
故选：B． （a-b）2 -3（a2+b2）
-2a2-2ab-2b2
【解析】试题分析：先根据完全平方公式计算，再合并同类项即可.
试题解析：
（a-b）2 -3（a2+b2）=a2-2ab+b2-3a2-3b2=-2a2-2ab-2b2. 下面计算正确的是（ ）
A. (a+b)(a-b)=2a+2b B. b5 + b5 = b10 C. x5 .x5 = x25 D. (y-z)2=y2-2yz+z2
D
【解析】选项A，原式=a2-b2 ；选项 B，原式=2b5；选项C，原式=x10 ;选项D，原式= y2-2yz+z2.故选D. 2（a-b）（a+b）-a2+b2
a2-b2
【解析】试题分析：先根据平方差公式计算，再合并同类项即可.
试题解析：
2（a-b）（a+b）-a2+b2=2a2-2b2-a2+b2=a2-b2. [（c·c2)+（a·a2)][（c·c2)-（a·a2)]等于（ ）
A. c3 -a3 B. c2 -a8 C. c5 -a5 D. c6 -a6
D
【解析】根据平方差公式和同底数幂的乘法法则可得：[（c·c2)+（a·a2)][（c·c2)-（a·a2)]= =c6 -a6，故选D. 下面计算错误的是（ ）
A. (y-z)(y+z)=y2-z2 B. (m-n)(m+n)=n2-m C. x5·x20 = x25 D. y3 · y5 = y8
B
【解析】根据平方差公式可得：选项A，(y-z)(y+z)=y2-z2；选项B， (m-n)(m+n)=m2-n2；根据同底数幂的乘法法则可得：选项C，x5·x20 = x25；选项D， y3 · y5 = y8.故选B. 已知直角三角形的直角边分别为5和12，则斜边上的中线为___________．
6.5
【解析】分两种情况：①5和12是两条直角边，根据勾股定理求得斜边为13，利用直角三角形斜边的中线等于斜边的一半即可得斜边上的中线的长度为6.5；②5是直角边，12为斜边，利用直角三角形斜边的中线等于斜边的一半即可得斜边上的中线的长度为6. 求使分式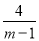
的值为整数的所有整数m的和．
6
【解析】利用整除的性质：即m－1是4的因数这一条件，即可求解.
【解析】
∵分式的值为整数，
∴m－1是4的因数，
又∵m为整数，
∴m＝5,3,2,0，－1，－3，
则它们的和为5＋3＋2＋0＋(－1)＋(－3)＝6.