题目内容
5.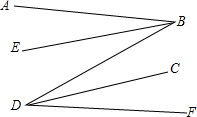 如图,AB∥DF,BE,DC分别是∠ABD,∠FDB的平分线,BE∥DC吗?为什么?
如图,AB∥DF,BE,DC分别是∠ABD,∠FDB的平分线,BE∥DC吗?为什么?解:由BE平分∠ABD,得∠DBE=∠ABE,同理可得∠BDC=∠FDC.
由于AB∥CD,根据两直线平行,内错角相等可得∠ABD=∠ABD=∠FDB.
因此∠DBE=∠BDC,根据内错角相等,两直线平行可得BE∥DC.
(提示:为了说理需要,可按自己喜欢的方式在图中标注)
分析 由角平分线得出:∠DBE=∠ABE,∠BDC=∠FDC,由平行线的性质得出∠ABD=∠FDB.证出∠DBE=∠BDC,由平行线的判定方法即可得出结论.
解答 解:由BE平分∠ABD,得:∠DBE=∠ABE,同理可得:∠BDC=∠FDC.
由于AB∥CD,根据两直线平行,内错角相等,可得∠ABD=∠FDB.
由于AB∥CD,根据两直线平行,内错角相等,可得∠ABD=∠FDB.
因此∠DBE=∠BDC,根据内错角相等,两直线平行,可得BE∥DC.
故答案为:∠DBE=∠ABE,∠BDC=∠FDC.
两直线平行,内错角相等,∠FDB.
∠DBE=∠BDC,内错角相等,两直线平行.
点评 本题考查了平行线的判定与性质、角平分线的定义;由平行线的性质和角平分线证出∠DBE=∠BDC是解决问题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
15.试计算|3-8|×(-2)的值为( )
| A. | 10 | B. | 7 | C. | -10 | D. | -7 |
20.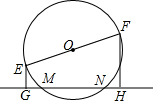 如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
 如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )| A. | 12cm | B. | 8cm | C. | 6cm | D. | 3cm |
 如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点B1,延长AA1到A2,使得A1A2=A1B1,连接A2B1,在A2B1上取一点B2,延长A1A2到A3,使得A2A3=A2B2;…,按此作法进行下去,∠A2015A2016B2015的度数为$\frac{80°}{{2}^{2015}}$.
如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点B1,延长AA1到A2,使得A1A2=A1B1,连接A2B1,在A2B1上取一点B2,延长A1A2到A3,使得A2A3=A2B2;…,按此作法进行下去,∠A2015A2016B2015的度数为$\frac{80°}{{2}^{2015}}$.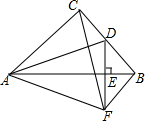 如图所示,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连结CF、AD.
如图所示,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连结CF、AD.