题目内容
15.先化简,再求值.$\frac{y}{x-y}+\frac{{y}^{3}}{x(x-y)^{2}}÷\frac{xy+{y}^{2}}{{y}^{2}-{x}^{2}}$,其中x=1,y=3.分析 首先把分式的分子和分母分解因式,把除法转化为乘法,计算乘法,然后通分相减即可化简,最后代入数值计算即可.
解答 解:原式=$\frac{y}{x-y}$+$\frac{{y}^{3}}{x(x-y)^{2}}$•$\frac{(x+y)(y-x)}{y(x+y)}$
=$\frac{y}{x-y}$-$\frac{{y}^{2}}{x(x-y)}$
=$\frac{xy-{y}^{2}}{x(x-y)}$
=$\frac{y(x-y)}{x(x-y)}$
=$\frac{y}{x}$,
当x=1,y=3时,原式=3.
点评 本题考查了分式的化简求值,正确进行通分、约分、分解因式是关键.

练习册系列答案
相关题目
14.抛物线y=2(x-1)2的对称轴是( )
| A. | 1 | B. | 直线x=1 | C. | 直线x=2 | D. | 直线x=-1 |
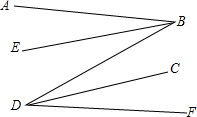 如图,AB∥DF,BE,DC分别是∠ABD,∠FDB的平分线,BE∥DC吗?为什么?
如图,AB∥DF,BE,DC分别是∠ABD,∠FDB的平分线,BE∥DC吗?为什么? 如图,AB=CB,∠ABC=60°,且∠EAB=∠FCB,∠ABC=∠FBE,∠CEB=30°.
如图,AB=CB,∠ABC=60°,且∠EAB=∠FCB,∠ABC=∠FBE,∠CEB=30°.