题目内容
20.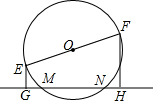 如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )| A. | 12cm | B. | 8cm | C. | 6cm | D. | 3cm |
分析 过O作OH′⊥MN,连接OM,根据垂径定理可得MH′=3cm,再利用勾股定理计算出OH′的长,然后根据梯形中位线定理可得答案.
解答 解:过O作OH′⊥MN,连接OM,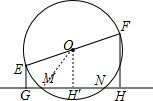
∵MN=6cm,
∴MH′=3cm,
∵EF=10cm,
∴MO=5cm,
∴OH′=$\sqrt{M{O}^{2}-M{H}^{2}}$=4cm,
∵O是EF中点,H′是MN中点,
∴HO是梯形EGH′HF的中位线,
∴EG+FH=2OH′=8cm,
∴E、F两点到直线MN的距离之和等于8cm,
故选:B.
点评 此题主要考查了梯形中位线定理,以及垂径定理,关键是掌握垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目
12.下列算式正确的是( )
| A. | ($\frac{a}{b}$)m=$\frac{{a}^{m}}{{b}^{m}}$ | B. | ($\frac{a+b}{b}$)2=$\frac{{a}^{2}+{b}^{2}}{{b}^{2}}$ | ||
| C. | (-$\frac{{y}^{3}}{{x}^{2}}$)2=-$\frac{{y}^{9}}{{x}^{4}}$ | D. | ($\frac{2x}{3y}$)4=$\frac{8{x}^{4}}{12{y}^{4}}$ |
 数a、b、c在数轴上对应的位置如图所示,化简|b-a|+|b-c|-|c|.
数a、b、c在数轴上对应的位置如图所示,化简|b-a|+|b-c|-|c|.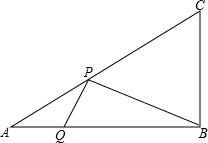 在△ABC中(AC>AB),∠A=30°,AB=2,P、Q分别为AC、AB上的点,求PB+PQ的最小值.
在△ABC中(AC>AB),∠A=30°,AB=2,P、Q分别为AC、AB上的点,求PB+PQ的最小值.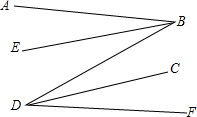 如图,AB∥DF,BE,DC分别是∠ABD,∠FDB的平分线,BE∥DC吗?为什么?
如图,AB∥DF,BE,DC分别是∠ABD,∠FDB的平分线,BE∥DC吗?为什么?