题目内容
14.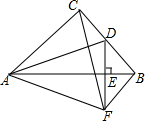 如图所示,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连结CF、AD.
如图所示,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连结CF、AD.(1)求证:△ACD≌△CBF;
(2)求证:AD⊥CF;
(3)连结AF,试判断△ACF的形状,并说明理由.
分析 (1)先证出CD=DB,BF=DB,得出BF=CD,再证出∠CBF=∠ACD,由BC=AC,即可证出Rt△CBF≌Rt△ACD(SAS);
(2)由Rt△CBF≌Rt△ACD得出∠BCF=∠CAD,从而证出∠AGC=90°,得出AD⊥CF;
(3)由(2)可得CF=AD,又AB垂直平分DF,可得AD=AF,可证明CF=AF,可知△ACF为等腰三角形.
解答 证明:(1)∵△ABC是等腰直角三角形,
∴AC=CB,∠CBA=∠CAB=45°,
∵DE⊥AB,
∴∠DEB=90°,∠BDE=45°,
又∵BF∥AC,
∴∠CBF=90°,
∴∠BFD=∠BDE=45°,∠BFD=∠ACD=90°,
∴BF=DB,
∵D为BC的中点,
∴CD=DB,
∴BF=CD,
在△CBF和△ACD中,
$\left\{\begin{array}{l}{BC=AC}\\{∠CBF=∠ACD}\\{BF=CD}\end{array}\right.$
∴△CBF≌△ACD(SAS);
(2)由(1)得△CBF≌△ACD,
∴∠BCF=∠CAD,
∵∠BCF+∠GCA=90°,
∴∠CAD+∠GCA=90°,即∠AGC=90°,
∴AD⊥CF;
(3)由(2)可知△ACD≌△CBF,
∴AD=CF,
由(1)可知AB垂直平分DF,
∴AD=AF,
∴AF=CF,
∴△ACF为等腰三角形.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(SSS、SAS、ASA、AAS和HL)和性质(全等三角形的对应边、对应角相等)是解题的关键.

练习册系列答案
相关题目
14.抛物线y=2(x-1)2的对称轴是( )
| A. | 1 | B. | 直线x=1 | C. | 直线x=2 | D. | 直线x=-1 |
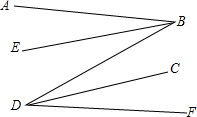 如图,AB∥DF,BE,DC分别是∠ABD,∠FDB的平分线,BE∥DC吗?为什么?
如图,AB∥DF,BE,DC分别是∠ABD,∠FDB的平分线,BE∥DC吗?为什么?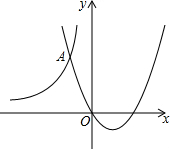 如图,抛物线y=(x-1)2-1与双曲线y=$\frac{k}{x}$交于点A(-1,m).
如图,抛物线y=(x-1)2-1与双曲线y=$\frac{k}{x}$交于点A(-1,m).