题目内容
10. 已知:如图,PM=PN,∠M=∠N.求证:AM=BN.
已知:如图,PM=PN,∠M=∠N.求证:AM=BN.分析:∵PM=PN,
∴要证AM=BN,只要证PA=PB,
只要证△PAN≌△PBM.
证明:在△PAN与△PBM中,
∠P=∠P(公共角)
PN=PM(已知)
∠N=∠M(已知)
∴△PAN≌△PBM(ASA).
∴PA=PB(全等三角形的对应边相等).
∵PM=PN (已知),
∴PM-PA=PN-PB,即AM=BN.
分析 欲证明AM=AN,因为PM=PN,只要证明PA=PB即可,只要证明△PAN≌△PBM.
解答 解:分析:∵PM=PN,∴要证AM=BN,只要证PA=PB, 只要证△PAN≌△PBM.
只要证△PAN≌△PBM.
证明:在△PAN和△PBM中,
$\left\{\begin{array}{l}{∠P=∠P}&{(公共角)}\\{PN=PN}&{(已知)}\\{∠N=∠M}&{(已知)}\end{array}\right.$,
∴△PAN≌△PBM(ASA)
∴PA=PB(全等三角形对应边相等)
∵PM=PN(已知)
∴PM-PA=PN-PB,即AM=BN.
故答案分别为:PB,△PAN,△PBM,PAN.PBM,P,P,公共角,PM,PN,已知,N,M,已知,PAN,PBM,ASA,PB,全等三角形对应边相等,已知,PA,PB,BN.
点评 本题考查全等三角形的判定和性质、解题的关键是熟练掌握全等三角形判定方法,属于基础题,中考常考题型.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
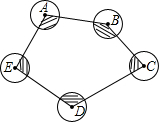 如图,五个半径为2的圆,圆心分别是点A,B,C,D,E,则图中阴影部分的面积和是多少?(S扇形=$\frac{nπR^2}{360°}$)
如图,五个半径为2的圆,圆心分别是点A,B,C,D,E,则图中阴影部分的面积和是多少?(S扇形=$\frac{nπR^2}{360°}$)