题目内容
 如图,每个小正方形都是边长为1个单位长度的正方形,△A′B′C′是由△ABC绕点O旋转180°后得到的图形.
如图,每个小正方形都是边长为1个单位长度的正方形,△A′B′C′是由△ABC绕点O旋转180°后得到的图形.(1)请在方格中确定旋转中心O的位置,并以O为坐标原点建立平面直角坐标系,写出点B′的坐标;
(2)画出△ABC关于纵轴对称的△A1B1C1;
(3)过点O、A1、B′三点的圆的半径长为
考点:作图-旋转变换,作图-轴对称变换
专题:
分析:(1)利用关于原点对称点的性质即可得出O点位置,进而建立坐标系;
(2)利用关于y轴对称点的性质得出对应点位置,进而得出答案;
(3)利用勾股定理逆定理得出△OA1B′是直角三角形,进而求出直角三角形外接圆半径长.
(2)利用关于y轴对称点的性质得出对应点位置,进而得出答案;
(3)利用勾股定理逆定理得出△OA1B′是直角三角形,进而求出直角三角形外接圆半径长.
解答: 解:(1)如图所示:O即为所求,点B′的坐标为:(-1,2);
解:(1)如图所示:O即为所求,点B′的坐标为:(-1,2);
(2)如图所示:△A1B1C1即为所求;
(3)∵A1O2=5,B′O2=5,A1B
=10,
∴△OA1B′是直角三角形,
∴过点O、A1、B′三点的圆的半径长为:
=
.
故答案为:
.
 解:(1)如图所示:O即为所求,点B′的坐标为:(-1,2);
解:(1)如图所示:O即为所求,点B′的坐标为:(-1,2);(2)如图所示:△A1B1C1即为所求;
(3)∵A1O2=5,B′O2=5,A1B
′2 |
∴△OA1B′是直角三角形,
∴过点O、A1、B′三点的圆的半径长为:
| A1B′ |
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:此题主要考查了轴对称变换以及勾股定理逆定理和旋转变换,得出O点位置是解题关键.

练习册系列答案
相关题目
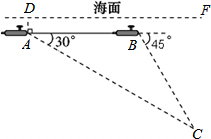 如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:
如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:
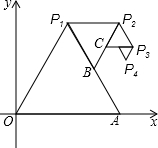 如图,以O(0,0)、A(2,0)为顶点作正△OAP1,以点P1和线段P1A的中点B为顶点作正△P1BP2,再以点P2和线段P2B的中点C为顶点作△P2CP3,…,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是
如图,以O(0,0)、A(2,0)为顶点作正△OAP1,以点P1和线段P1A的中点B为顶点作正△P1BP2,再以点P2和线段P2B的中点C为顶点作△P2CP3,…,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是 如图,AB是⊙O的直径,以AB为一边作等边△ABC,交⊙O于点E、F,联结AF,若AB=4,则图中阴影部分的面积为
如图,AB是⊙O的直径,以AB为一边作等边△ABC,交⊙O于点E、F,联结AF,若AB=4,则图中阴影部分的面积为 根据去年某班学生体育毕业考试的成绩(成绩取整数),制成如图所示的频数分布直方图,若成绩在24.5~27.5分范围内为良好,则该班学生体育成绩良好的百分率是
根据去年某班学生体育毕业考试的成绩(成绩取整数),制成如图所示的频数分布直方图,若成绩在24.5~27.5分范围内为良好,则该班学生体育成绩良好的百分率是