题目内容
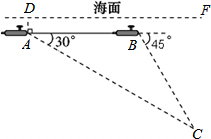 如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:
如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:| 2 |
| 3 |
| 5 |
考点:解直角三角形的应用-仰角俯角问题
专题:几何图形问题
分析:首先作CE⊥AB于E,依题意,AB=1000,∠EAC=30°,∠CBE=45°,设CD=x,则BE=x,进而利用正切函数的定义求出x即可.
解答: 解:作CE⊥AB于E,
解:作CE⊥AB于E,
依题意,AB=1464,∠EAC=30°,∠CBE=45°,
设CE=x,则BE=x,
Rt△ACE中,tan30°=
=
=
,
整理得出:3x=1464
+
x,
解得:x=732(
+1)≈2000米,
∴C点深度=x+600=2600米.
答:海底C点处距离海面DF的深度约为2600米.
 解:作CE⊥AB于E,
解:作CE⊥AB于E,依题意,AB=1464,∠EAC=30°,∠CBE=45°,
设CE=x,则BE=x,
Rt△ACE中,tan30°=
| CE |
| AE |
| x |
| 1464+x |
| ||
| 3 |
整理得出:3x=1464
| 3 |
| 3 |
解得:x=732(
| 3 |
∴C点深度=x+600=2600米.
答:海底C点处距离海面DF的深度约为2600米.
点评:此题主要考查了俯角的定义及其解直角三角形的应用,解题时首先正确理解俯角的定义,然后利用三角函数和已知条件构造方程解决问题.

练习册系列答案
相关题目
 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.

 如图,每个小正方形都是边长为1个单位长度的正方形,△A′B′C′是由△ABC绕点O旋转180°后得到的图形.
如图,每个小正方形都是边长为1个单位长度的正方形,△A′B′C′是由△ABC绕点O旋转180°后得到的图形.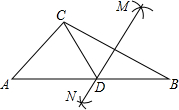 如图,在△ABC中,按以下步骤作图:
如图,在△ABC中,按以下步骤作图: