题目内容
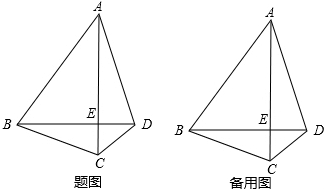
如图,在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,∠ADB=∠CAD+∠ABD,∠BAD=3∠CBD.
(1)求证:△ABC为等腰三角形;
(2)M是线段BD上一点,BM:AB=3:4,点F在BA的延长线上,连接FM,∠BFM的平分线FN交BD于点N,交AD于点G,点H为BF中点,连接MH,当GN=GD时,探究线段CD、FM、MH之间的数量关系,并证明你的结论.
(1)求证:△ABC为等腰三角形;
(2)M是线段BD上一点,BM:AB=3:4,点F在BA的延长线上,连接FM,∠BFM的平分线FN交BD于点N,交AD于点G,点H为BF中点,连接MH,当GN=GD时,探究线段CD、FM、MH之间的数量关系,并证明你的结论.

考点:相似形综合题,平行线的判定与性质,等腰三角形的判定与性质,直角三角形的性质,相似三角形的判定与性质
专题:压轴题
分析:(1)根据等式的性质,可得∠APE=∠ADE,根据等腰三角形的性质,可得∠PAD=2β,根据直角三角形的性质,可得∠AEB+∠CBE=90°,根据等式的性质,可得∠ABC=∠ACB,根据等腰三角形的判定,可得答案;
(2)根据相似三角形的判定与性质,可得∠ABE=∠ACD,根据等腰三角形的性质,可得∠GND=∠GDN,根据对顶角的性质,可得∠AGF的度数,根据三角形外角的性质,∠AFG的度数,根据直角三角形的性质,可得BF与MH的关系,根据等腰三角形的性质,可得∠FRM=∠FMR,根据平行线的判定与性质,可得∠CBD=∠RMB,根据相似三角形的判定与性质,可得
=
=
=
,根据线段的和差,可得BR=BF-FR,根据等量代换,可得答案.
(2)根据相似三角形的判定与性质,可得∠ABE=∠ACD,根据等腰三角形的性质,可得∠GND=∠GDN,根据对顶角的性质,可得∠AGF的度数,根据三角形外角的性质,∠AFG的度数,根据直角三角形的性质,可得BF与MH的关系,根据等腰三角形的性质,可得∠FRM=∠FMR,根据平行线的判定与性质,可得∠CBD=∠RMB,根据相似三角形的判定与性质,可得
| BR |
| CD |
| BM |
| AC |
| AM |
| AB |
| 3 |
| 4 |
解答:(1)证明:如图1,作∠BAP=∠DAE,AP交BD于P,
设∠CBD=α,∠CAD=β,
∵∠ADB=∠CAD+∠ABD,∠APE=∠BAP+∠ABD,
∴∠APE=∠ADE,AP=AD.
∵AC⊥BD
∴∠PAE=∠DAE=β,
∴∠PAD=2β,∠BAD=3β.
∵∠BAD=3∠CBD,
∴3β=3α,β=α.
∵AC⊥BD,
∴∠ACB=90°-∠CBE=90°-α=90°-β.
∵∠ABC=180°-∠BAC-∠ACB=90°-β,
∴∠ACB=∠ABC,
∴△ABC为等腰三角形;
(2)2MH=FM+
CD.
证明:如图2,
由(1)知AP=AD,AB=AC,∠BAP=∠CAD=β,
∴△ABP≌△ACD,
∴∠ABE=∠ACD.
∵AC⊥BD,
∴∠GDN=90°-β,
∵GN=GD,
∴∠GND=∠GDN=90°-β,
∴∠NGD=180°-∠GND-∠GDN=2β.
∴∠AGF=∠NGD=2β.
∴∠AFG=∠BAD-∠AGF=3β-2β=β.
∵FN平分∠BFM,
∴∠NFM=∠AFG=β,
∴FM∥AE,
∴∠FMN=90°.
∵H为BF的中点,
∴BF=2MH.
在FB上截取FR=FM,连接RM,
∴∠FRM=∠FMR=90°-β.
∵∠ABC=90°-β,
∴∠FRM=∠ABC,
∴RM∥BC,
∴∠CBD=∠RMB.
∵∠CAD=∠CBD=β,
∴∠RMB=∠CAD.
∵∠RBM=∠ACD,
∴△RMB∽△DAC,
∴
=
=
=
,
∴BR=
CD.
∵BR=FB-FM,
∴FB-FM=BR=
CD,
FB=FM+
CD.
∴2MH=FM+
CD.

设∠CBD=α,∠CAD=β,
∵∠ADB=∠CAD+∠ABD,∠APE=∠BAP+∠ABD,
∴∠APE=∠ADE,AP=AD.
∵AC⊥BD
∴∠PAE=∠DAE=β,
∴∠PAD=2β,∠BAD=3β.
∵∠BAD=3∠CBD,
∴3β=3α,β=α.
∵AC⊥BD,
∴∠ACB=90°-∠CBE=90°-α=90°-β.
∵∠ABC=180°-∠BAC-∠ACB=90°-β,
∴∠ACB=∠ABC,
∴△ABC为等腰三角形;
(2)2MH=FM+
| 3 |
| 4 |

证明:如图2,
由(1)知AP=AD,AB=AC,∠BAP=∠CAD=β,
∴△ABP≌△ACD,
∴∠ABE=∠ACD.
∵AC⊥BD,
∴∠GDN=90°-β,
∵GN=GD,
∴∠GND=∠GDN=90°-β,
∴∠NGD=180°-∠GND-∠GDN=2β.
∴∠AGF=∠NGD=2β.
∴∠AFG=∠BAD-∠AGF=3β-2β=β.
∵FN平分∠BFM,
∴∠NFM=∠AFG=β,
∴FM∥AE,
∴∠FMN=90°.
∵H为BF的中点,
∴BF=2MH.
在FB上截取FR=FM,连接RM,
∴∠FRM=∠FMR=90°-β.
∵∠ABC=90°-β,
∴∠FRM=∠ABC,
∴RM∥BC,
∴∠CBD=∠RMB.
∵∠CAD=∠CBD=β,
∴∠RMB=∠CAD.
∵∠RBM=∠ACD,
∴△RMB∽△DAC,
∴
| BR |
| CD |
| BM |
| AC |
| BM |
| AB |
| 3 |
| 4 |
∴BR=
| 3 |
| 4 |
∵BR=FB-FM,
∴FB-FM=BR=
| 3 |
| 4 |
FB=FM+
| 3 |
| 4 |
∴2MH=FM+
| 3 |
| 4 |
点评:本题考查了相似形综合题,(1)利用了等腰三角形的性质,等腰三角形的判定,直角三角形的性质;(2)相似三角形的判定与性质,直角三角形的性质,三角形外角的性质,平行线的判定与性质,利用的知识点多,题目稍有难度,相似三角形的判定与性质是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知等腰三角形的其中二边长分别为4,9,则这个等腰三角形的周长为( )
| A、17 | B、22 |
| C、17或22 | D、无法确定 |
 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠BCD.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠BCD. 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
 如图,每个小正方形都是边长为1个单位长度的正方形,△A′B′C′是由△ABC绕点O旋转180°后得到的图形.
如图,每个小正方形都是边长为1个单位长度的正方形,△A′B′C′是由△ABC绕点O旋转180°后得到的图形.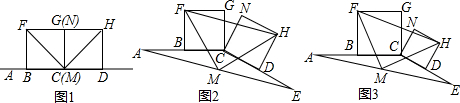
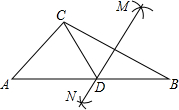 如图,在△ABC中,按以下步骤作图:
如图,在△ABC中,按以下步骤作图: