Question

16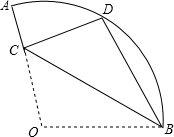．已知：如图，在扇形OAB中，∠AOB=110°，半径OA=18，将扇形OAB沿过点B的直线折叠，点O恰好落在$\widehat{AB}$上的点D处，折痕交OA于点C，则$\widehat{AD}$的长为（　　）

• A． 2π
• B． 3π
• C． 4π
• D． 5π

Answer 1

分析 如图，连接OD．根据折叠的性质、圆的性质推知△ODB是等边三角形，则易求∠AOD=110°-∠DOB=50°；然后由弧长公式弧长的公式l=$\frac{nπr}{180}$来求$\widehat{AD}$的长．

解答 解：如图，连接OD．
根据折叠的性质知，OB=DB．
又∵OD=OB，
∴OD=OB=DB，即△ODB是等边三角形，
∴∠DOB=60°．
∵∠AOB=110°，
∴∠AOD=∠AOB-∠DOB=50°，
∴$\widehat{AD}$的长为$\frac{50π×18}{180}$=5π．
故选：D．

点评 本题考查了弧长的计算，翻折变换（折叠问题）．折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．所以由折叠的性质推知△ODB是等边三角形是解答此题的关键之处．