题目内容
6. 如图,?ABCD中,AB=14,BC=17,其中一边上的高为15,∠B为锐角,则tanB等于( )
如图,?ABCD中,AB=14,BC=17,其中一边上的高为15,∠B为锐角,则tanB等于( )| A. | $\frac{8}{15}$ | B. | $\frac{15}{8}$ | C. | 15 | D. | $\frac{15}{8}$或15 |
分析 首先由?ABCD中,AB=14,BC=17,其中一边上的高为15,易得此高是边CD上的高,然后分别过点A作AE⊥CD于点E,利用勾股定理求得DE的长,继而求得tanB的值.
解答  解:分别过点A作AE⊥CD于点E,
解:分别过点A作AE⊥CD于点E,
∵?ABCD中,AB=14,BC=17,
∴AD=BC=17,CD=AB=14,∠B=∠D,
∵其中一边上的高为15,
∴此高是边CD上的高,则AE=15,
∴ED=$\sqrt{A{D}^{2}-A{E}^{2}}$=8,
∴tanB=tanD=$\frac{AE}{BE}$=$\frac{15}{8}$.
故选B.
点评 此题考查了平行四边形的性质以及锐角三角函数的定义.注意确定此高是边CD上的高是关键.

练习册系列答案
相关题目
16.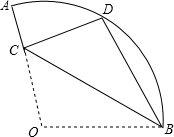 已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长为( )
已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长为( )
 已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长为( )
已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长为( )| A. | 2π | B. | 3π | C. | 4π | D. | 5π |
18. 如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是( )
如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是( )
 如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是( )
如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是( )| A. | 16 | B. | 24 | C. | 32 | D. | 48 |
15. 如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )
如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )
 如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )
如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )| A. | △ACD的外心 | B. | △ABC的外心 | C. | △ACD的内心 | D. | △ABC的内心 |
16.下列运算结果正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a6 | C. | a3÷a2=a | D. | (a2)3=a5 |
 为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.