题目内容
1. 折叠矩形ABCD,使点D落在BC边上的点F处,若折痕AE=5$\sqrt{5}$,tan∠EFC=$\frac{3}{4}$,则BC=10.
折叠矩形ABCD,使点D落在BC边上的点F处,若折痕AE=5$\sqrt{5}$,tan∠EFC=$\frac{3}{4}$,则BC=10.
分析 根据tan∠EFC=$\frac{3}{4}$,设CE=3k,在RT△EFC中可得CF=4k,EF=DE=5k,根据∠BAF=∠EFC,利用三角函数的知识求出AF,然后在RT△AEF中利用勾股定理求出k,继而代入可得出答案.
解答 解:设CE=3k,则CF=4k,由勾股定理得EF=DE=$\sqrt{C{E}^{2}+C{F}^{2}}$=5k,
∴DC=AB=8k,
∵∠AFB+∠BAF=90°,∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
∴tan∠BAF=tan∠EFC=$\frac{3}{4}$,
∴BF=6k,AF=BC=AD=10k,
在Rt△AFE中,由勾股定理得AE=$\sqrt{A{F}^{2}+E{F}^{2}}$=$\sqrt{125{k}^{2}}$=5$\sqrt{5}$k=5$\sqrt{5}$,
解得:k=1,
∴BC=10×1=10;
故答案为:10.
点评 此题考查了翻折变换的性质、矩形的性质、勾股定理;解答本题关键是根据三角函数值,表示出每条线段的长度,然后利用勾股定理进行解答,有一定难度.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
12. 如图所示,直线m∥n,则∠α为( )
如图所示,直线m∥n,则∠α为( )
 如图所示,直线m∥n,则∠α为( )
如图所示,直线m∥n,则∠α为( )| A. | 70° | B. | 55° | C. | 50° | D. | 30° |
16.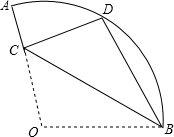 已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长为( )
已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长为( )
 已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长为( )
已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长为( )| A. | 2π | B. | 3π | C. | 4π | D. | 5π |
10.为了建设一个整洁、文明的城市,某校组织了以“讲文明、守秩序”知识竞赛活动从中抽取了5名同学的参赛成绩如下(单位:分):80,90,70,100,80,则这组数据中位数和众数分别是( )
| A. | 90,80 | B. | 70,80 | C. | 80,80 | D. | 100,80 |
 如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.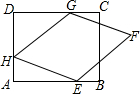 如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分別在矩形ABCD的边AB、CD、DA上,AH=2.
如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分別在矩形ABCD的边AB、CD、DA上,AH=2. 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.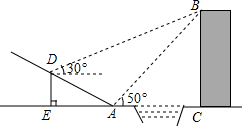 如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)
如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数) 为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.