题目内容
7．正六边形的边心距是$\sqrt{3}$，则它的边长是（ ）| A． | $\frac{\sqrt{3}}{3}$ | B． | 2 | C． | $\sqrt{3}$ | D． | $\frac{2}{3}$$\sqrt{3}$ |
分析 运用正六边形的性质，正六边形边长等于外接圆的半径，再利用勾股定理解决．
解答 
解：∵正六边形的边心距为$\sqrt{3}$，
∴OB=$\sqrt{3}$，AB=$\frac{1}{2}$OA，
∵OA2=AB2+OB2，
∴OA2=（$\frac{1}{2}$OA）2+（$\sqrt{3}$）2，
解得：OA=2．
故选B．
点评 本题考查了正六边形和圆，掌握外接圆的半径等于正六边形的边长是解此题的关键．
练习册系列答案
相关题目
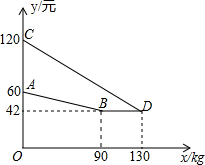某企业生产并销售某种产品，假设销售量与产量相等，如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1（单位：元）、销售价y2（单位：元）与产量x（单位：kg）之间的函数关系．
某公司销售A，B两种产品，根据市场调研，确定两条信息：
12．
如图所示，直线m∥n，则∠α为（ ）
如图所示，直线m∥n，则∠α为（ ）| A． | 70° | B． | 55° | C． | 50° | D． | 30° |
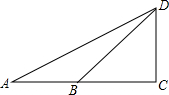小明准备用所学数学知识测量广场上旗杆CD的高度，如图所示，在底面A处测得顶端的仰角为25.5°，在B处测得仰角为36.9°，已知点A、B、C在同一直线上，量得AB=10米．求旗杆的高度．
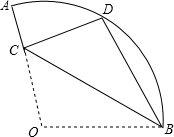已知：如图，在扇形OAB中，∠AOB=110°，半径OA=18，将扇形OAB沿过点B的直线折叠，点O恰好落在$\widehat{AB}$上的点D处，折痕交OA于点C，则$\widehat{AD}$的长为（ ）