题目内容
8. 如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为1或$\frac{\sqrt{3}}{3}$.
如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为1或$\frac{\sqrt{3}}{3}$.
分析 分两种情况:①过A′作MN∥CD交AD于M,交BC于N,则直线MN是矩形ABCD 的对称轴,得出AM=BN=$\frac{1}{2}$AD=1,由勾股定理得到A′N=0,求得A′M=1,再由勾股定理解得A′E即可;
②过A′作PQ∥AD交AB于P,交CD于Q;求出∠EBA′=30°,由三角函数求出AE=A′E=A′B×tan30°;即可得出结果.
解答 解:分两种情况:
①如图1,过A′作MN∥CD交AD于M,交BC于N,
则直线MN是矩形ABCD 的对称轴,
∴AM=BN=$\frac{1}{2}$AD=1,
∵△ABE沿BE折叠得到△A′BE,
∴A′E=AE,A′B=AB=1,
∴A′N=$\sqrt{A′{B}^{2}-B{N}^{2}}$=0,即A′与N重合,
∴A′M=1,
∴A′E2=EM2+A′M2,
∴A′E2=(1-A′E)2+12,
解得:A′E=1,
∴AE=1;
②如图2, 过A′作PQ∥AD交AB于P,交CD于Q,
过A′作PQ∥AD交AB于P,交CD于Q,
则直线PQ是矩形ABCD 的对称轴,
∴PQ⊥AB,AP=PB,AD∥PQ∥BC,
∴A′B=2PB,
∴∠PA′B=30°,
∴∠A′BC=30°,
∴∠EBA′=30°,∴AE=A′E=A′B×tan30°=1×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$;
综上所述:AE的长为1或$\frac{\sqrt{3}}{3}$;
故答案为:1或$\frac{\sqrt{3}}{3}$.
点评 本题考查了翻折变换-折叠问题,矩形的性质,勾股定理;正确理解折叠的性质是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
16.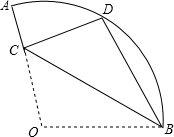 已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长为( )
已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长为( )
 已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长为( )
已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长为( )| A. | 2π | B. | 3π | C. | 4π | D. | 5π |
18. 如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是( )
如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是( )
 如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是( )
如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是( )| A. | 16 | B. | 24 | C. | 32 | D. | 48 |
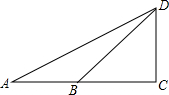 小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.
小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度. 如图所示,BA和CD表示前后两幢楼,按照有感规定两幢楼间的间距不得小于楼的高度,即图中AC大于等于CD,小明想测量一下他家所著AB楼与前面CD楼是否符合规定,于是他在AC间的点M处架了测角仪,测得CD楼顶D的仰角为45°,已知AM=4米,测角仪距地面MN=1.5米.
如图所示,BA和CD表示前后两幢楼,按照有感规定两幢楼间的间距不得小于楼的高度,即图中AC大于等于CD,小明想测量一下他家所著AB楼与前面CD楼是否符合规定,于是他在AC间的点M处架了测角仪,测得CD楼顶D的仰角为45°,已知AM=4米,测角仪距地面MN=1.5米.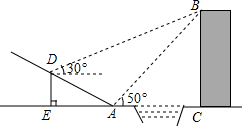 如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)
如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数) 如图,将矩形纸片P折叠,使点A与点C重合,折痕为EF,若AB=8,BC=4.则:
如图,将矩形纸片P折叠,使点A与点C重合,折痕为EF,若AB=8,BC=4.则: