题目内容
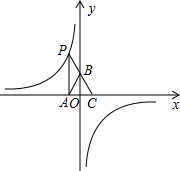 如图,点P是反比例函数y=
如图,点P是反比例函数y=| k |
| x |
| 5 |
考点:反比例函数图象上点的坐标特征
专题:
分析:根据题意过点P作PE⊥y轴于点E,得出△PBE≌△CBO(AAS),进而求出P点坐标即可得出答案.
解答: 解:过点P作PE⊥y轴于点E,
解:过点P作PE⊥y轴于点E,
∵PA垂直x轴于点A(-1,0),点C的坐标为(1,0),
∴PE=CO=AO=1,
∵AB=
,
∴BO=2,
在△PBE和△CBO中
∵
,
∴△PBE≌△CBO(AAS),
∴BE=BO=2,
∴P点坐标为:(-1,4),
∴k=-1×4=-4.
故答案为:-4.
 解:过点P作PE⊥y轴于点E,
解:过点P作PE⊥y轴于点E,∵PA垂直x轴于点A(-1,0),点C的坐标为(1,0),
∴PE=CO=AO=1,
∵AB=
| 5 |
∴BO=2,
在△PBE和△CBO中
∵
|
∴△PBE≌△CBO(AAS),
∴BE=BO=2,
∴P点坐标为:(-1,4),
∴k=-1×4=-4.
故答案为:-4.
点评:此题主要考查了反比例函数图象上点的坐标特点,得出P点纵坐标是解题关键.

练习册系列答案
相关题目
 己知a,b两数在数轴上对应的点如图所示,则|a|+|a-b|等于( )
己知a,b两数在数轴上对应的点如图所示,则|a|+|a-b|等于( )| A、-a | B、-b |
| C、b-2a | D、2a-b |
 如图,AB=AC,AD=AE,则图中所有全等三角形共有( )
如图,AB=AC,AD=AE,则图中所有全等三角形共有( )| A、3对 | B、4对 | C、5对 | D、6对 |
 △ABC在直角坐标系中的位置如图所示,∠C=90°,点C的坐标为(
△ABC在直角坐标系中的位置如图所示,∠C=90°,点C的坐标为(| 3 |
| 2 |
| ||
| 2 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,0) |
 教练对小明推铅球的录像进行技术分析(如图),发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-
教练对小明推铅球的录像进行技术分析(如图),发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-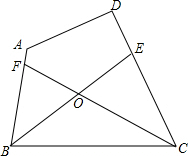 已知如图,在四边形ABCD中,∠ABC的平分线BE交CD于E,∠BCD的平分线CE交AB于F,BE、CF相交于O,∠A=124°,∠D=100°.求∠BOF的度数.
已知如图,在四边形ABCD中,∠ABC的平分线BE交CD于E,∠BCD的平分线CE交AB于F,BE、CF相交于O,∠A=124°,∠D=100°.求∠BOF的度数.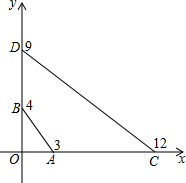 已知如图,A,B,C,D四点的坐标分别是(3,0),(0,4),(12,0),(0,9),探索∠OBA和∠OCD的大小关系,并说明理由.
已知如图,A,B,C,D四点的坐标分别是(3,0),(0,4),(12,0),(0,9),探索∠OBA和∠OCD的大小关系,并说明理由.