题目内容
5.若三角形的三边长为5、12、13,求其外接圆的半径和其内切圆的直径.分析 先根据勾股定理的逆定理求出△ABC是直角三角形,然后利用直角边为a、b,斜边为c的三角形的内切圆半径为$\frac{a+b-c}{2}$,外接圆的半径为$\frac{c}{2}$进行计算即可.
解答 解:∵△ABC的三边长分别为5、12、13,
∴52+122=132,
∴△ABC是直角三角形,
∴△ABC的外接圆的半径R=$\frac{13}{2}$=6.5,
△ABC的内切圆半径r=$\frac{5+12-13}{2}$=2,
∴△ABC的内切圆的直径是4.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.记住直角边为a、b,斜边为c的三角形的内切圆半径为$\frac{a+b-c}{2}$,外接圆的半径为$\frac{c}{2}$.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列计算中,正确的是( )
| A. | x3•x2=x4 | B. | x(x-2)=-2x+x2 | C. | (x+y)(x-y)=x2+y2 | D. | 3x3y2÷xy2=3x4 |
13.为了节约资源,科学指导居民改善居住条件,小强向房管部门提出了一个购买商品房的政策性方案:
设一个3口之家购买商品房的人均面积为x平方米,缴纳房款y万元.
(1)请求出y关于x的函数关系式;
(2)若某3人之家欲购买120平方米的商品房,求其应缴纳的房款.
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30(平方米)部分 | 0.4 |
| 超过30平方米部分 | 0.9 |
(1)请求出y关于x的函数关系式;
(2)若某3人之家欲购买120平方米的商品房,求其应缴纳的房款.
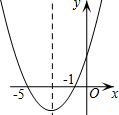 如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2-4ac>0;④a+b+c<0;⑤对于图象上的两点(-6,m )、(1,n),有m<n.其中正确信息的个数有( )
如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2-4ac>0;④a+b+c<0;⑤对于图象上的两点(-6,m )、(1,n),有m<n.其中正确信息的个数有( )