题目内容
6.把一个圆分割成三个扇形,它们圆心角的度数比为1:2:3,求最大的扇形的圆心角的度数.分析 首先根据题意,求出最大的扇形的圆心角占圆周角的$\frac{3}{1+2+3}$=$\frac{1}{2}$;然后根据分数乘法的意义,用360°乘以$\frac{1}{2}$,求出最大的扇形的圆心角的度数是多少即可.
解答 解:360°×$\frac{3}{1+2+3}$
=360°×$\frac{1}{2}$
=180°.
即最大的扇形的圆心角的度数是180°.
点评 此题主要考查了角的概念的应用,要熟练掌握,解答此题的关键是要明确:圆周角等于360°,并能判断出最大的扇形的圆心角的度数占圆周角的几分之几.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
20.对于实数x,我们规定:[x]表示不小于x的最小整数,例如:[1.4]=2,[4]=4,[-3.2]=-3,若[$\frac{x+3}{10}$]=6,则x的取值可以是( )
| A. | 41 | B. | 47 | C. | 50 | D. | 58 |
18.如图,∠1和∠2是同位角的是( )
| A. | 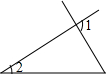 | B. | 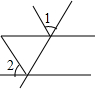 | C. | 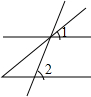 | D. | 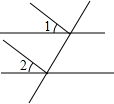 |
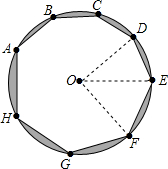 同圆或等圆中,圆心角互余的两个扇形叫做互余共轭扇形.如图⊙O内接八边形中,已知AB=BC=CD=DE=2,EF=FG=GH=HA=2$\sqrt{2}$.
同圆或等圆中,圆心角互余的两个扇形叫做互余共轭扇形.如图⊙O内接八边形中,已知AB=BC=CD=DE=2,EF=FG=GH=HA=2$\sqrt{2}$.