题目内容
2.已知关于x的方程x2-4x+3a-1=0有两个实数根.(1)求实数a的取值范围;
(2)若a为正整数,求方程的根.
分析 (1)由关于x的方程x2-4x+3a-1=0有两个实数根,根据判别式得到关于a的不等式,然后解不等式即可求出a的取值范围;
(2)根据(1)的结果和a为正整数可求特殊的a值,然后方程的解就可以求出.
解答 解:(1)∵关于x的方程x2-4x+3a-1=0有两个实数根,
∴△=(-4)2-4(3a-1)≥0,
解得a≤$\frac{5}{3}$,
∴a的取值范围为a≤$\frac{5}{3}$;
(2)∵a≤$\frac{5}{3}$,且a为正整数,
∴a=1,
∴方程x2-4x+3a-1=0可化为x2-4x+2=0.
∴此方程的根为x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$.
点评 本题考查了一元二次方程根的判别式(△=b2-4ac),一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
也考查了一元二次方程的解法.

练习册系列答案
相关题目
10.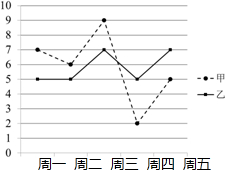 甲和乙入选学校的定点投篮大赛,他们每天训练后投10个球测试,记录命中的个数,五天后将记录的数据绘制成折线统计图,如图所示.则下列对甲、乙数据描述正确的是( )
甲和乙入选学校的定点投篮大赛,他们每天训练后投10个球测试,记录命中的个数,五天后将记录的数据绘制成折线统计图,如图所示.则下列对甲、乙数据描述正确的是( )
 甲和乙入选学校的定点投篮大赛,他们每天训练后投10个球测试,记录命中的个数,五天后将记录的数据绘制成折线统计图,如图所示.则下列对甲、乙数据描述正确的是( )
甲和乙入选学校的定点投篮大赛,他们每天训练后投10个球测试,记录命中的个数,五天后将记录的数据绘制成折线统计图,如图所示.则下列对甲、乙数据描述正确的是( )| A. | 甲的方差比乙的方差大 | B. | 甲的方差比乙的方差小 | ||
| C. | 甲的平均数比乙的平均数小 | D. | 甲的平均数比乙的平均数大 |
7.在下列图形中,既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
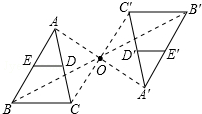 如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知BC=6,则E′D′=3.
如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知BC=6,则E′D′=3.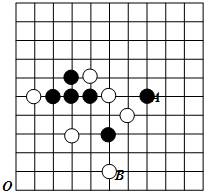 五子棋是一种两人对弈的棋类游戏,规则是:在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者为胜.如图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为(5,1);为了不让白方获胜,此时黑方应该下在坐标为(3,7)或(7,3)的位置处.
五子棋是一种两人对弈的棋类游戏,规则是:在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者为胜.如图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为(5,1);为了不让白方获胜,此时黑方应该下在坐标为(3,7)或(7,3)的位置处.