题目内容
二次函数y=-
(x+2)2-2,开口方向向 ,当x≥-2时,y随x的增大而 .
| 1 |
| 3 |
考点:二次函数的性质
专题:
分析:由a决定抛物线开口方向向下,又由抛物线的对称轴x=-2,可得当x≥-2时,y随x的增大而减小.
解答:解:∵二次函数-
<0,
∴抛物线开口方向向下,
又∵抛物线的对称轴x=-2,
∴当x≥-2时,y随x的增大而减小.
故答案为:下,减小.
| 1 |
| 3 |
∴抛物线开口方向向下,
又∵抛物线的对称轴x=-2,
∴当x≥-2时,y随x的增大而减小.
故答案为:下,减小.
点评:本题主要考查了二次函数的性质,解题的关键是熟记a决定抛物线开口方向.结合对称轴得出函数的增减性.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 实数a,b在数轴上的位置如图所示,则式子
实数a,b在数轴上的位置如图所示,则式子| a2 |
| b2 |
| A、a+b | B、a-b |
| C、-a-b | D、-a+b |
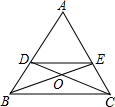 在△ABC中,AB=AC,BE,CD分别是∠ABC,∠ACB的平分线,则下列结论不正确的是( )
在△ABC中,AB=AC,BE,CD分别是∠ABC,∠ACB的平分线,则下列结论不正确的是( )| A、△OBC是等腰三角形 |
| B、△DBE是等腰三角形 |
| C、△DCE是等腰三角形 |
| D、△ACD是等腰三角形 |
 如图,∠AOB=90°,∠BOC=30°,OP平分∠AOC,OQ平分∠BOC,则∠POQ=
如图,∠AOB=90°,∠BOC=30°,OP平分∠AOC,OQ平分∠BOC,则∠POQ= 观察函数y=
观察函数y= 如图,是某物体的主视图和俯视图,依据此物体的主视图和俯视图找出符合该物体的左视图( )
如图,是某物体的主视图和俯视图,依据此物体的主视图和俯视图找出符合该物体的左视图( )



 如图,已知菱形ABCD中,对角线AC、BD交于O点,AB=10,BD=12,则AC=
如图,已知菱形ABCD中,对角线AC、BD交于O点,AB=10,BD=12,则AC= 如图所示,有一根高为2m的木柱,它的底面周长为0.3m,为了营造喜庆的气氛,老师要求小明将一根彩带从柱底向柱顶均匀地缠绕7圈,一直缠到起点的正上方为止.问:小明至少需要准备一根多长的彩带?
如图所示,有一根高为2m的木柱,它的底面周长为0.3m,为了营造喜庆的气氛,老师要求小明将一根彩带从柱底向柱顶均匀地缠绕7圈,一直缠到起点的正上方为止.问:小明至少需要准备一根多长的彩带?