题目内容
8.若三角形的三边长分别是下列各组数,则能构成直角三角形的是( )| A. | 4,5,6 | B. | 1,2,$\sqrt{5}$ | C. | 6,8,11 | D. | 5,12,14 |
分析 根据判断三条线段是否能构成直角三角形的三边,需验证两小边的平方和是否等于最长边的平方,分别对每一项进行分析,即可得出答案.
解答 解:A、42+52≠62,不符合勾股定理的逆定理,不是直角三角形;
B、12+22=($\sqrt{5}$)2,符合勾股定理的逆定理,是直角三角形;
C、62+82≠112,不符合勾股定理的逆定理,不是直角三角形;
D、52+122≠142,不符合勾股定理的逆定理,不是直角三角形.
故选B.
点评 本题主要考查了勾股定理的逆定理:用到的知识点是已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.

练习册系列答案
相关题目
18.函数y=$\sqrt{x-3}$中自变量x的取值范围是( )
| A. | x≤3 | B. | x≠3 | C. | x≠-3 | D. | x≥3 |
16.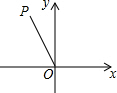 如图,已知∠POx=120°,OP=4,则点P的坐标是( )
如图,已知∠POx=120°,OP=4,则点P的坐标是( )
 如图,已知∠POx=120°,OP=4,则点P的坐标是( )
如图,已知∠POx=120°,OP=4,则点P的坐标是( )| A. | (2,4) | B. | (-2,4) | C. | (-2,2$\sqrt{3}$) | D. | (-2$\sqrt{3}$,2) |
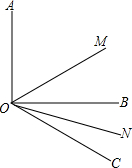 (1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;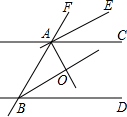 如图,直线AC∥BD,AE、AO、BO分别是∠CAF、∠BAC、∠ABD的平分线.求证:
如图,直线AC∥BD,AE、AO、BO分别是∠CAF、∠BAC、∠ABD的平分线.求证: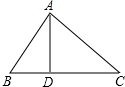 如图,在△ABC中,AB=15,AC=20,BC=25,AD是BC边上的高,
如图,在△ABC中,AB=15,AC=20,BC=25,AD是BC边上的高, 如图,一次函数y=kx+b(k≠0)与坐标轴交于点A,B,则△AOB的面积为4.
如图,一次函数y=kx+b(k≠0)与坐标轴交于点A,B,则△AOB的面积为4.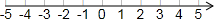 (1)先化简,再求值:(x+3)(x-3)-x(x-2),其中x=4.
(1)先化简,再求值:(x+3)(x-3)-x(x-2),其中x=4.