题目内容
13.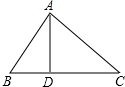 如图,在△ABC中,AB=15,AC=20,BC=25,AD是BC边上的高,
如图,在△ABC中,AB=15,AC=20,BC=25,AD是BC边上的高,(1)判断△ABC的形状,并说明理由;
(2)求AD的长.
分析 (1)△ABC为直角三角形,利用勾股定理的逆定理证明即可;
(2)根据三角形ABC的面积为定值即可求出AD的长.
解答 解:(1)△ABC为直角三角形,
理由如下:
∵AB=15,AC=20,BC=25
∴AB2+AC2=625,
∵BC2=625,
∴AB2+AC2=BC2,
∴∠BAC=90°
∴△ABC是直角三角形;
(2)∵S△ABC=$\frac{1}{2}$AB×AC=$\frac{1}{2}$AD×BC,
∴$\frac{1}{2}$×15×20=$\frac{1}{2}$×AD×25,
∴AD=12.
点评 本题考查了勾股定理以及其逆定理的运用,解决本题的关键在于利用两个直角三角形的公共边找到突破点.主要利用了勾股定理进行解答.

练习册系列答案
相关题目
4.若|a|=3,|b|=4,且ab<0,则a+b的值是( )
| A. | 1 | B. | -7 | C. | 7或-7 | D. | 1或-1 |
1. 已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线与边BC交于点D、与对角线OB交于点中点E,若△OBD的面积为10,则k的值是( )
已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线与边BC交于点D、与对角线OB交于点中点E,若△OBD的面积为10,则k的值是( )
 已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线与边BC交于点D、与对角线OB交于点中点E,若△OBD的面积为10,则k的值是( )
已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线与边BC交于点D、与对角线OB交于点中点E,若△OBD的面积为10,则k的值是( )| A. | 10 | B. | 5 | C. | $\frac{10}{3}$ | D. | $\frac{20}{3}$ |
8.若三角形的三边长分别是下列各组数,则能构成直角三角形的是( )
| A. | 4,5,6 | B. | 1,2,$\sqrt{5}$ | C. | 6,8,11 | D. | 5,12,14 |
18.已知:在平面直角坐标系中,菱形ABCD三个顶点的坐标分别是A(-2,0)、B(0,1)、C(2,0),则点D的坐标是( )
| A. | (-4,-1) | B. | (4,-1) | C. | (0,-1) | D. | (0,-2) |
 如图,E、F是?ABCD对角线AC上的两点,AF=CE.求证:BE=DF.
如图,E、F是?ABCD对角线AC上的两点,AF=CE.求证:BE=DF.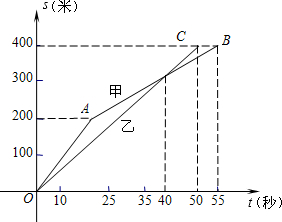 如图,在甲、乙两同学进行的400米跑步比赛中,路程s(米)与时间t(秒)之间函数关系的图象分别为折线OAB和线段OC,根据图象提供的信息回答以下问题:
如图,在甲、乙两同学进行的400米跑步比赛中,路程s(米)与时间t(秒)之间函数关系的图象分别为折线OAB和线段OC,根据图象提供的信息回答以下问题: 如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.
如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.