题目内容
3.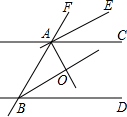 如图,直线AC∥BD,AE、AO、BO分别是∠CAF、∠BAC、∠ABD的平分线.求证:
如图,直线AC∥BD,AE、AO、BO分别是∠CAF、∠BAC、∠ABD的平分线.求证:(1)AE∥BO;
(2)AE⊥AO.
分析 (1)根据角平分线的定义和平行线的判定证明即可;
(2)根据角平分线的定义和垂直的定义证明即可.
解答 证明:(1)∵AC∥BD,∠FAC=∠ABD,
∵AE、AO、BO分别是∠CAF、∠BAC、∠ABD的平分线,
∴∠FAE=$\frac{1}{2}$∠FAC,∠ABO=$\frac{1}{2}$∠ABD,
∴∠FAE=∠ABO,
∴AE∥BO;
(2)∵AE、AO、BO分别是∠CAF、∠BAC、∠ABD的平分线,
∴∠FAE=∠EAC,∠CAO=∠OAB,
∴∠FAE+∠OAB=∠EAC+∠CAO,
∵∠FAE+∠OAB+∠EAC+∠CAO=180°,
∴∠EAC+∠CAO=90°,
∴AE⊥AO.
点评 此题考查平行线的判定,关键是根据角平分线的定义、垂直的定义和平行线的判定证明.

练习册系列答案
相关题目
8.若三角形的三边长分别是下列各组数,则能构成直角三角形的是( )
| A. | 4,5,6 | B. | 1,2,$\sqrt{5}$ | C. | 6,8,11 | D. | 5,12,14 |
15.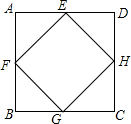 如图,点E、F、G、H是正方形ABCD各边的中点,则四边形EFGH( )
如图,点E、F、G、H是正方形ABCD各边的中点,则四边形EFGH( )
 如图,点E、F、G、H是正方形ABCD各边的中点,则四边形EFGH( )
如图,点E、F、G、H是正方形ABCD各边的中点,则四边形EFGH( )| A. | 是轴对称图形但不是中心对称图形 | B. | 既是轴对称图形又是中心对称图形 | ||
| C. | 是中心对称图形但不是轴对称图形 | D. | 没有对称性 |
13.某商场用18万元购进A、B两种商品,其进价和售价如下表:
(1)若销售完后共获利3万元,该商场购进A、B两种商品各多少件;
(2)若购进B种商品的件数不少于A种商品的件数的6倍,且每种商品都必须购进.
①问共有几种进货方案?
②要保证利润最高,你选择哪种进货方案?
| A | B | |
| 进价(元/件) | 1200 | 1000 |
| 售价(元/件) | 1380 | 1200 |
(2)若购进B种商品的件数不少于A种商品的件数的6倍,且每种商品都必须购进.
①问共有几种进货方案?
②要保证利润最高,你选择哪种进货方案?
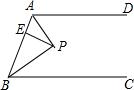 如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为( )
如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为( )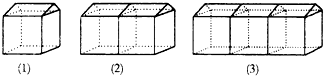 搭建如图(1)的单顶帐篷需要17根钢管,这样的帐篷按图(2)、(3)的方式串起来搭建,则串8顶这样的帐篷需要94根钢管.
搭建如图(1)的单顶帐篷需要17根钢管,这样的帐篷按图(2)、(3)的方式串起来搭建,则串8顶这样的帐篷需要94根钢管.