题目内容
19.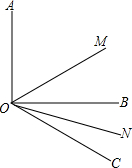 (1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;(2)如果(1)中的∠AOB=α,∠BOC=β,其它条件不变,请用求α或β来表示∠MON的度数.
分析 (1)根据角平分线的定义得到∠MOC=$\frac{1}{2}$∠AOC,∠NOC=$\frac{1}{2}$∠BOC,则∠MON=∠MOC-∠NOC=$\frac{1}{2}$(∠AOC-∠BOC)=$\frac{1}{2}$∠AOB,然后把∠AOB的度数代入计算即可;
(2)由∠AOB=α,∠BOC=β,得到∠AOC=∠AOB+∠BOC=α+β,根据OM平分∠AOC,ON平分∠BOC,于是得到∠MOC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$(α+β),∠NOC=$\frac{1}{2}$∠BOC=$\frac{1}{2}$β,即可得到结果.
解答 解:(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=90°+30°=120°,
又∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=$\frac{1}{2}$∠AOC=60°,∠NOC=$\frac{1}{2}$∠BOC=15°,
∴∠MON=∠MOC-∠NOC=60°-15°=45°,
(2)∵∠AOB=α,∠BOC=β,
∴∠AOC=∠AOB+∠BOC=α+β,
又∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$(α+β),∠NOC=$\frac{1}{2}$∠BOC=$\frac{1}{2}$β,
∴∠MON=∠MOC-∠NOC=$\frac{1}{2}$(α+β)-$\frac{1}{2}$β=$\frac{1}{2}$α.
点评 本题考查的是角平分线的定义,熟知角平分线的定义是解答此题的关键.

练习册系列答案
相关题目
10.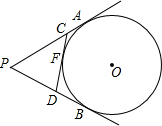 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则$\frac{OA}{PA}$的值是( )
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则$\frac{OA}{PA}$的值是( )
 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则$\frac{OA}{PA}$的值是( )
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则$\frac{OA}{PA}$的值是( )| A. | $\frac{2}{13}\sqrt{13}$ | B. | $\frac{12}{5}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
7.-2013的相反数是( )
| A. | -$\frac{1}{2013}$ | B. | $\frac{1}{2013}$ | C. | -2013 | D. | 2013 |
4.若|a|=3,|b|=4,且ab<0,则a+b的值是( )
| A. | 1 | B. | -7 | C. | 7或-7 | D. | 1或-1 |
8.若三角形的三边长分别是下列各组数,则能构成直角三角形的是( )
| A. | 4,5,6 | B. | 1,2,$\sqrt{5}$ | C. | 6,8,11 | D. | 5,12,14 |