题目内容
17.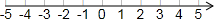 (1)先化简,再求值:(x+3)(x-3)-x(x-2),其中x=4.
(1)先化简,再求值:(x+3)(x-3)-x(x-2),其中x=4.(2)解不等式组$\left\{\begin{array}{l}{2x-3≤1}\\{\frac{1}{2}x+1>0}\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)根据平方差公式和整式的乘法化简合并代入求值即可;
(2)分别解出两个不等式的解集,取其公共解集即可.
解答 解:(1)(x+3)(x-3)-x(x-2)
=x2-9-x2+2x
=2x-9,
把x=4代入2x-9=8-9=-1;
(2)解不等式①得:x≤2,
解不等式②得:x>-2,
所以不等式组的解集为:-2<x≤2,
数轴上表示为:
点评 此题考查不等式组的解法,关键是分别解出两个不等式的解集,取其公共解集.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
7.-2013的相反数是( )
| A. | -$\frac{1}{2013}$ | B. | $\frac{1}{2013}$ | C. | -2013 | D. | 2013 |
8.若三角形的三边长分别是下列各组数,则能构成直角三角形的是( )
| A. | 4,5,6 | B. | 1,2,$\sqrt{5}$ | C. | 6,8,11 | D. | 5,12,14 |
6.二次函数y=3+2(x+1)2的图象的最低点的坐标为( )
| A. | (3,-1) | B. | (-1,3) | C. | (1,3) | D. | (0,5) |
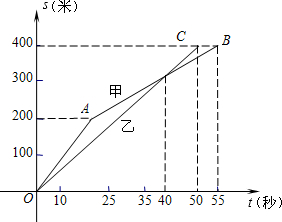 如图,在甲、乙两同学进行的400米跑步比赛中,路程s(米)与时间t(秒)之间函数关系的图象分别为折线OAB和线段OC,根据图象提供的信息回答以下问题:
如图,在甲、乙两同学进行的400米跑步比赛中,路程s(米)与时间t(秒)之间函数关系的图象分别为折线OAB和线段OC,根据图象提供的信息回答以下问题: 如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.
如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.