题目内容
18.已知关于x、y的二元一次方程组$\left\{\begin{array}{l}{3x+5y=6}\\{3x+ky=10}\end{array}\right.$给出下列结论:①当k=5时,此方程组无解;②若此方程组的解也是方程6x+15y=16的解,则k=10;③无论整数k取何值,此方程组一定无整数解(x、y均为整数),其中正确的是( )| A. | ①②③ | B. | ①③ | C. | ②③ | D. | ①② |
分析 ①将k=5代入,得到方程组$\left\{\begin{array}{l}{3x+5y=6}\\{3x+5y=10}\end{array}\right.$,求解即可做出判断;
②解方程组$\left\{\begin{array}{l}{3x+5y=6}\\{3x+10y=10}\end{array}\right.$得:$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{4}{5}}\end{array}\right.$,把x=$\frac{2}{3}$,y=$\frac{4}{5}$代入6x+15y=16,即可做出判断;
③解方程组$\left\{\begin{array}{l}{3x+5y=6}\\{3x+ky=10}\end{array}\right.$得:$\left\{\begin{array}{l}{x=2-\frac{20}{3k-15}}\\{y=\frac{4}{k-5}}\end{array}\right.$,根据k为整数即可作出判断.
解答 解:∵当k=5时,方程组为$\left\{\begin{array}{l}{3x+5y=6}\\{3x+5y=10}\end{array}\right.$,此时方程组无解;∴①正确;
∵解方程组$\left\{\begin{array}{l}{3x+5y=6}\\{3x+10y=10}\end{array}\right.$得:$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{4}{5}}\end{array}\right.$,
把x=$\frac{2}{3}$,y=$\frac{4}{5}$代入6x+15y=16,方程左右两边相等,∴②正确;
∵解方程组$\left\{\begin{array}{l}{3x+5y=6}\\{3x+ky=10}\end{array}\right.$得:$\left\{\begin{array}{l}{x=2-\frac{20}{3k-15}}\\{y=\frac{4}{k-5}}\end{array}\right.$,
又∵k为整数,
∴x、y不能均为整数,∴③正确.
故选:A.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.

 阅读快车系列答案
阅读快车系列答案| A. | 4,5,6 | B. | 1,2,$\sqrt{5}$ | C. | 6,8,11 | D. | 5,12,14 |
| A. | (3,-1) | B. | (-1,3) | C. | (1,3) | D. | (0,5) |
| A | B | |
| 进价(元/件) | 1200 | 1000 |
| 售价(元/件) | 1380 | 1200 |
(2)若购进B种商品的件数不少于A种商品的件数的6倍,且每种商品都必须购进.
①问共有几种进货方案?
②要保证利润最高,你选择哪种进货方案?
| A. | 容量,方差 | B. | 平均数,容量 | C. | 容量,平均数 | D. | 方差、平均数 |
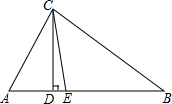 如图,在Rt△ABC中,CD为斜边AB上的高,且AD=2厘米,BD=8厘米,求:
如图,在Rt△ABC中,CD为斜边AB上的高,且AD=2厘米,BD=8厘米,求: